Page 330 - Physical chemistry understanding our chemical world

INTRODUCTION TO CELLS: TERMINOLOGY AND BACKGROUND 297

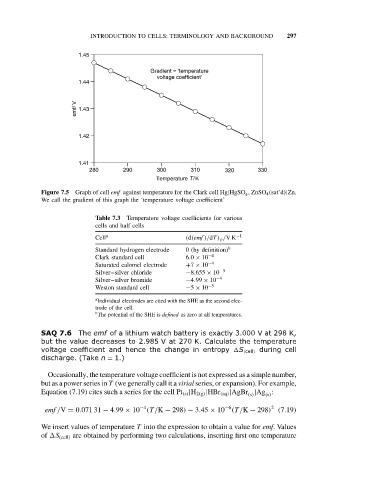
1.45
Gradient = ‘temperature
voltage coefficient’
1.44

emf/ V 1.43

1.42

1.41
280 290 300 310 320 330
Temperature T/K
Figure 7.5 Graph of cell emf against temperature for the Clark cell Hg|HgSO , ZnSO 4 (sat’d)|Zn.
4
We call the gradient of this graph the ‘temperature voltage coefficient’

Table 7.3 Temperature voltage coefficients for various
cells and half cells

Cell a (d(emf )/dT) p /VK −1
Standard hydrogen electrode 0 (by definition) b
Clark standard cell 6.0 × 10 −4
Saturated calomel electrode +7 × 10 −4
Silver–silver chloride −8.655 × 10 −5
Silver–silver bromide −4.99 × 10 −4
Weston standard cell −5 × 10 −5
a Individual electrodes are cited with the SHE as the second elec-
trode of the cell.
b The potential of the SHE is defined as zero at all temperatures.

SAQ 7.6 The emf of a lithium watch battery is exactly 3.000 V at 298 K,
but the value decreases to 2.985 V at 270 K. Calculate the temperature
voltage coefficient and hence the change in entropy S (cell) during cell
discharge. (Take n = 1.)

Occasionally, the temperature voltage coefficient is not expressed as a simple number,
but as a power series in T (we generally call it a virial series, or expansion). For example,
Equation (7.19) cites such a series for the cell Pt (s) |H 2(g) |HBr (aq) |AgBr |Ag :
(s) (s)

2
−6
−4
emf /V = 0.071 31 − 4.99 × 10 (T/K − 298) − 3.45 × 10 (T/K − 298) (7.19)
We insert values of temperature T into the expression to obtain a value for emf. Values
of S (cell) are obtained by performing two calculations, inserting first one temperature