Page 352 - Physical chemistry understanding our chemical world

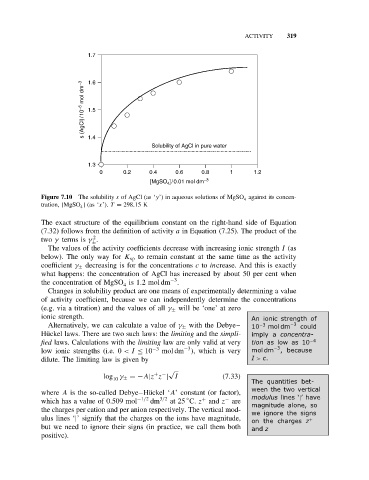
ACTIVITY 319

1.7

s (AgCl)/10 −5 mol dm −3 1.6

1.5

1.4
Solubility of AgCl in pure water

1.3
0 0.2 0.4 0.6 0.8 1 1.2
]/0.01 mol dm −3
[MgSO 4
Figure 7.10 The solubility s of AgCl (as ‘y’) in aqueous solutions of MgSO against its concen-
4
tration, [MgSO ](as ‘x’). T = 298.15 K
4
The exact structure of the equilibrium constant on the right-hand side of Equation
(7.32) follows from the definition of activity a in Equation (7.25). The product of the
2
two γ terms is γ .
±
The values of the activity coefficients decrease with increasing ionic strength I (as
below). The only way for K sp to remain constant at the same time as the activity
coefficient γ ± decreasing is for the concentrations c to increase. And this is exactly
what happens: the concentration of AgCl has increased by about 50 per cent when
−3
the concentration of MgSO is 1.2 mol dm .
4
Changes in solubility product are one means of experimentally determining a value
of activity coefficient, because we can independently determine the concentrations
(e.g. via a titration) and the values of all γ ± will be ‘one’ at zero
ionic strength. An ionic strength of
Alternatively, we can calculate a value of γ ± with the Debye– 10 −3 mol dm −3 could
H¨ uckel laws. There are two such laws: the limiting and the simpli- imply a concentra-
fied laws. Calculations with the limiting law are only valid at very tion as low as 10 −4
−3
low ionic strengths (i.e. 0 <I ≤ 10 −3 mol dm ), which is very mol dm −3 ,because
dilute. The limiting law is given by I > c.
√
+ −
log γ ± =−A|z z | I (7.33)
10
The quantities bet-
ween the two vertical
where A is the so-called Debye–H¨ uckel ‘A’ constant (or factor),
◦
−
which has a value of 0.509 mol −1/2 dm 3/2 at 25 C. z and z are modulus lines ‘|’have
+
magnitude alone, so
the charges per cation and per anion respectively. The vertical mod-
we ignore the signs
ulus lines ‘|’ signify that the charges on the ions have magnitude, on the charges z +
but we need to ignore their signs (in practice, we call them both and z −
positive).