Page 128 - Process Equipment and Plant Design Principles and Practices by Subhabrata Ray Gargi Das

5.3 Multi-stream problem 125

Hot composite
curve
ΔT (original)
Pinch min
ΔT
T (°C) min

Cold composite
curve (original)

Cold composite
curve (shifted)
q – q rec q +
H
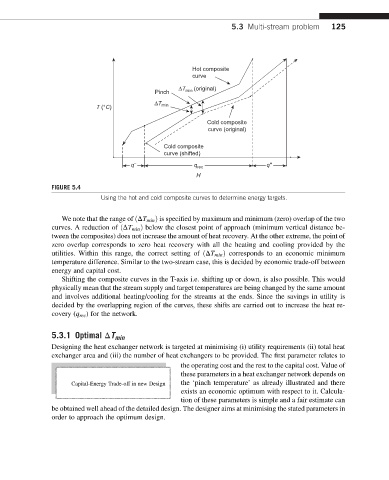
FIGURE 5.4
Using the hot and cold composite curves to determine energy targets.

We note that the range of ðDT min Þ is specified by maximum and minimum (zero) overlap of the two
curves. A reduction of ðDT min Þ below the closest point of approach (minimum vertical distance be-
tween the composites) does not increase the amount of heat recovery. At the other extreme, the point of
zero overlap corresponds to zero heat recovery with all the heating and cooling provided by the
utilities. Within this range, the correct setting of ðDT min Þ corresponds to an economic minimum
temperature difference. Similar to the two-stream case, this is decided by economic trade-off between
energy and capital cost.
Shifting the composite curves in the T-axis i.e. shifting up or down, is also possible. This would
physically mean that the stream supply and target temperatures are being changed by the same amount
and involves additional heating/cooling for the streams at the ends. Since the savings in utility is
decided by the overlapping region of the curves, these shifts are carried out to increase the heat re-
covery (q rec ) for the network.

5.3.1 Optimal DT min

Designing the heat exchanger network is targeted at minimising (i) utility requirements (ii) total heat
exchanger area and (iii) the number of heat exchangers to be provided. The first parameter relates to
the operating cost and the rest to the capital cost. Value of
these parameters in a heat exchanger network depends on
Capital-Energy Trade-off in new Design the ‘pinch temperature’ as already illustrated and there
exists an economic optimum with respect to it. Calcula-
tion of these parameters is simple and a fair estimate can
be obtained well ahead of the detailed design. The designer aims at minimising the stated parameters in
order to approach the optimum design.