Page 157 - Process Modelling and Simulation With Finite Element Methods

144 Process Modelling and Simulation with Finife Element Methods

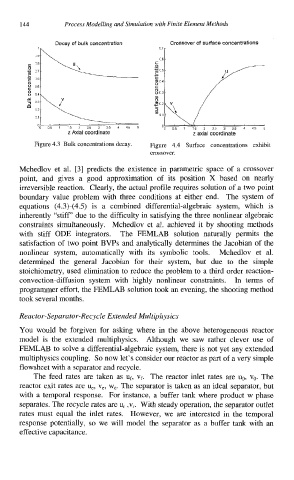
Decay of bulk concentration Crossover of surface concentratlons

Figure 4.3 Buk concentrations decay. Figure 4.4 Surface concentrations exhibit
crossover.
Mchedlov et al. [3] predicts the existence in parametric space of a crossover
point, and gives a good approximation of its position X based on nearly
irreversible reaction. Clearly, the actual profile requires solution of a two point
boundary value problem with three conditions at either end. The system of
equations (4.3)-(4.5) is a combined differential-algebraic system, which is
inherently “stiff’ due to the difficulty in satisfying the three nonlinear algebraic
constraints simultaneously. Mchedlov et al. achieved it by shooting methods
with stiff ODE integrators. The FEMLAB solution naturally permits the
satisfaction of two point BVPs and analytically determines the Jacobian of the
nonlinear system, automatically with its symbolic tools. Mchedlov et al.
determined the general Jacobian for their system, but due to the simple
stoichiometry, used elimination to reduce the problem to a third order reaction-
convection-diffusion system with highly nonlinear constraints. In terms of
programmer effort, the FEMLAB solution took an evening, the shooting method
took several months.

Reactor-Separator-Recycle Extended Multiphysics
You would be forgiven for asking where in the above heterogeneous reactor
model is the extended multiphysics. Although we saw rather clever use of
FEMLAB to solve a differential-algebraic system, there is not yet any extended
multiphysics coupling. So now let’s consider our reactor as part of a very simple
flowsheet with a separator and recycle.
The feed rates are taken as uf, vf. The reactor inlet rates are UO, VO. The
reactor exit rates are u,, v,, we. The separator is taken as an ideal separator, but
with a temporal response. For instance, a buffer tank where product w phase
separates. The recycle rates are u, ,vr. With steady operation, the separator outlet
rates must equal the inlet rates. However, we are interested in the temporal
response potentially, so we will model the separator as a buffer tank with an
effective capacitance.