Page 197 - Process Modelling and Simulation With Finite Element Methods

184 Process Modelling and Simulation with Finite Element Methods

Surface: temperature (T) Arrow: velocity [u,v] 103

06

04
03
02
01
-2
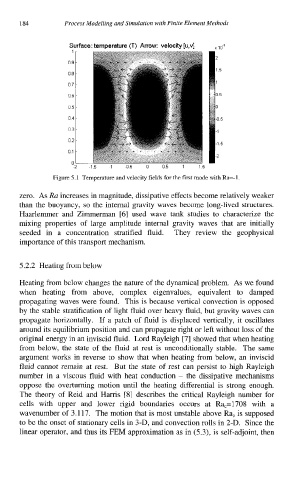
Figure 5.1 Temperature and velocity fields for the first mode with Ra=-l .

zero. As Ra increases in magnitude, dissipative effects become relatively weaker
than the buoyancy, so the internal gravity waves become long-lived structures.
Haarlemmer and Zimmerman [6] used wave tank studies to characterize the
mixing properties of large amplitude internal gravity waves that are initially
seeded in a concentration stratified fluid. They review the geophysical
importance of this transport mechanism.

5.2.2 Heating from below
Heating from below changes the nature of the dynamical problem. As we found
when heating from above, complex eigenvalues, equivalent to damped
propagating waves were found. This is because vertical convection is opposed
by the stable stratification of light fluid over heavy fluid, but gravity waves can
propagate horizontally. If a patch of fluid is displaced vertically, it oscillates
around its equilibrium position and can propagate right or left without loss of the
original energy in an inviscid fluid. Lord Rayleigh [7] showed that when heating
from below, the state of the fluid at rest is unconditionally stable. The same
argument works in reverse to show that when heating from below, an inviscid
fluid cannot remain at rest. But the state of rest can persist to high Rayleigh
number in a viscous fluid with heat conduction - the dissipative mechanisms
oppose the overturning motion until the heating differential is strong enough.
The theory of Reid and Harris [8] describes the critical Rayleigh number for
cells with upper and lower rigid boundaries occurs at Ra,=1708 with a
wavenumber of 3.117. The motion that is most unstable above Ra, is supposed
to be the onset of stationary cells in 3-D, and convection rolls in 2-D. Since the
linear operator, and thus its FEM approximation as in (5.3), is self-adjoint, then