Page 239 - Process Modelling and Simulation With Finite Element Methods

226 Process Modelling and Simulation with Finite Element Methods

AP
-=1.0 + 0.6155 E - 1.472 E~ + 6.955 E~
4
Although (6.6) fits the data well in the range shown, over the whole range, a
Laurent series in inverse powers of (1-E) gives a better fit to the ~=0.75 model
than the cubic of (6.6), when the fit is only done on the range E E [0,0.5].

-_ Ap 1= 0.395652 E - 0.3832 E~ (6.7)
APO (1-&13
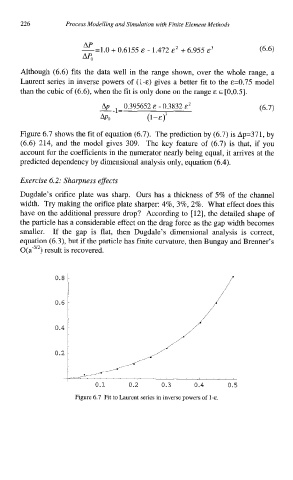
Figure 6.7 shows the fit of equation (6.7). The prediction by (6.7) is Ap=371, by
(6.6) 214, and the model gives 309. The key feature of (6.7) is that, if you
account for the coefficients in the numerator nearly being equal, it arrives at the
predicted dependency by dimensional analysis only, equation (6.4).

Exercise 6.2: Sharpness effects

Dugdale’s orifice plate was sharp. Ours has a thickness of 5% of the channel
width. Try malung the orifice plate sharper: 4%, 3%, 2%. What effect does this
have on the additional pressure drop? According to [12], the detailed shape of
the particle has a considerable effect on the drag force as the gap width becomes
smaller. If the gap is flat, then Dugdale’s dimensional analysis is correct,
equation (6.3), but if the particle has finite curvature, then Bungay and Brenner’s
O(a-5’2) result is recovered.

0.1 0.2 0.3 0.4 0.5
Figure 6.7 Fit to Laurent series in inverse powers of I-&.