Page 91 - Radiochemistry and nuclear chemistry

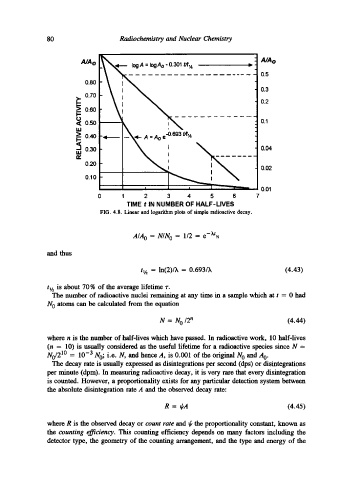
80 Radiochemistry and Nuclear Chemistry

: A/Ao
AJA~ = IogAo "0.301 tA'~ -
--- 0.5
0.80
- 0.3
>. 0.70
_ ~ - 0.2
>_. 0.60
I..-
t3 - 0.1
< 0.50 --- = :
> =
0.40 -- A = Ao e~O'693 f/t'A
-
tu 0.30 I - 0.04
IZ, I
0.20 i
i I - 0.02
._...-
0.10
0.01
0 1 2 3 4 5 6 7
TIME t IN NUMBER OF HALF-LIVES
FIG. 4.8. Linear and logarithm plots of simple radioactive decay.

AIA 0 = N/N 0 = 1/2 = e- Xt,~
and thus

tt~ = ln(2)/X = 0.693/X (4.43)
t,/= is about 70% of the average lifetime r.
The number of radioactive nuclei remaining at any time in a sample which at t = 0 had
N O atoms can be calculated from the equation

N = N O/2 n (4.44)

where n is the number of half-lives which have passed. In radioactive work, 10 half-lives
(n = 10) is usually considered as the useful lifetime for a radioactive species since N =
NO/210 = 10 -3 No; i.e. N, and hence A, is 0.001 of the original N O and A 0.
The decay rate is usually expressed as disintegrations per second (dps) or disintegrations
per minute (dpm). In measuring radioactive decay, it is very rare that every disintegration
is counted. However, a proportionality exists for any particular detection system between
the absolute disintegration rate A and the observed decay rate:

R = ~kA (4.45)

where R is the observed decay or count rate and 6 the proportionality constant, known as
the counting efficiency. This counting efficiency depends on many factors including the
detector type, the geometry of the counting arrangement, and the type and energy of the