Page 300 - Renewable Energy Devices and System with Simulations in MATLAB and ANSYS

Marine and Hydrokinetic Power Generation and Power Plants 287

Output power (kW) and rotational speed (rpm)
2000 50
1800 P (kW)-C pmax 45
1600 wr (rpm) 40
1400 35
1200 30
1000 25
800 20
600 15
400 10
200 5
0 0
0 1 2 3 4 5
Water flow (m/s)

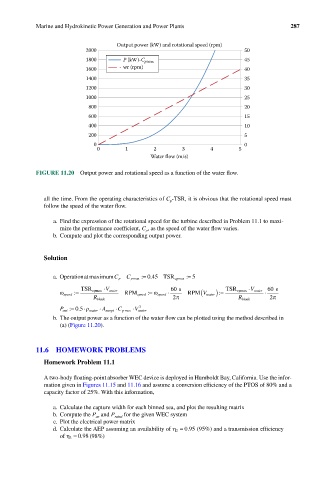
FIGURE 11.20 Output power and rotational speed as a function of the water flow.

all the time. From the operating characteristics of C p -TSR, it is obvious that the rotational speed must
follow the speed of the water flow.

a. Find the expression of the rotational speed for the turbine described in Problem 11.1 to maxi-
mize the performance coefficient, C p , as the speed of the water flow varies.
b. Compute and plot the corresponding output power.

Solution

.
a. OperationatmaximumC p C pmax := 045 TSR cpmax := 5
V ⋅ 60 s V ⋅ water 60 s
ω speed := TSR cpmax water RPM speed := ω speed ⋅ RPM( V wateer) =: TSR cpmax ⋅
R blade 2 π R blade 2π
. ⋅
3
P out := 05 ρ water ⋅ A swept ⋅ C pmax ⋅ V water
b. The output power as a function of the water flow can be plotted using the method described in
(a) (Figure 11.20).

11.6 HOMEWORK PROBLEMS
Homework Problem 11.1

A two-body floating-point absorber WEC device is deployed in Humboldt Bay, California. Use the infor-
mation given in Figures 11.15 and 11.16 and assume a conversion efficiency of the PTOS of 80% and a
capacity factor of 25%. With this information,

a. Calculate the capture width for each binned sea, and plot the resulting matrix
b. Compute the P ae and P rated for the given WEC system
c. Plot the electrical power matrix
.
d. Calculate the AEP assuming an availability of η 2 = 095 (95%) and a transmission efficiency
of η 3 = 098 (98%)
.