Page 21 - Schaum's Outline of Theory and Problems of Electric Circuits

10
2.4 RESISTANCE CIRCUIT CONCEPTS [CHAP. 2

All electrical devices that consume energy must have a resistor (also called a resistance) in their
circuit model. Inductors and capacitors may store energy but over time return that energy to the source
2 2
or to another circuit element. Power in the resistor, given by p ¼ vi ¼ i R ¼ v =R, is always positive as
illustrated in Example 2.1 below. Energy is then determined as the integral of the instantaneous power
ð ð ð
t 2 t 2 1 t 2
2 2
w ¼ pdt ¼ R i dt ¼ v dt
R
t 1 t 1 t 1
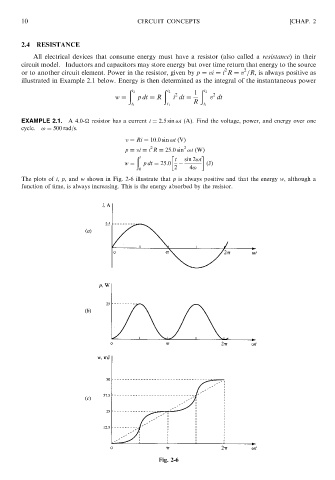
EXAMPLE 2.1. A 4.0-
resistor has a current i ¼ 2:5 sin !t (A). Find the voltage, power, and energy over one
cycle. ! ¼ 500 rad/s.
v ¼ Ri ¼ 10:0 sin !t ðVÞ
2
2
p ¼ vi ¼ i R ¼ 25:0 sin !t ðWÞ
ð
t t sin 2!t
w ¼ pdt ¼ 25:0 ðJÞ
0 2 4!
The plots of i, p, and w shown in Fig. 2-6 illustrate that p is always positive and that the energy w, although a
function of time, is always increasing. This is the energy absorbed by the resistor.

Fig. 2-6