Page 22 - Schaum's Outline of Theory and Problems of Electric Circuits

CHAP. 2]
2.5 INDUCTANCE CIRCUIT CONCEPTS 11

The circuit element that stores energy in a magnetic field is an inductor (also called an inductance).
With time-variable current, the energy is generally stored during some parts of the cycle and then
returned to the source during others. When the inductance is removed from the source, the magnetic
field will collapse; in other words, no energy is stored without a connected source. Coils found in electric
motors, transformers, and similar devices can be expected to have inductances in their circuit models.
Even a set of parallel conductors exhibits inductance that must be considered at most frequencies. The
power and energy relationships are as follows.

di d 1 2
p ¼ vi ¼ L i ¼ Li
dt dt 2
ð ð
t 2 t 2 1 2 2
w L ¼ pdt ¼ Li dt ¼ L½i 2 i 1 Š
2
t 1 t 1
2
1
Energy stored in the magnetic field of an inductance is w L ¼ Li .
2
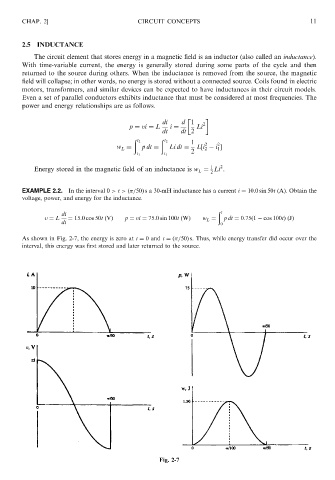
EXAMPLE 2.2. In the interval 0 > t > ð =50Þ s a 30-mH inductance has a current i ¼ 10:0 sin 50t (A). Obtain the
voltage, power, and energy for the inductance.
ð
di t
v ¼ L ¼ 15:0 cos 50t ðVÞ p ¼ vi ¼ 75:0 sin 100t ðWÞ w L ¼ pdt ¼ 0:75ð1 cos 100tÞðJÞ
dt 0

As shown in Fig. 2-7, the energy is zero at t ¼ 0 and t ¼ð =50Þ s. Thus, while energy transfer did occur over the
interval, this energy was first stored and later returned to the source.

Fig. 2-7