Page 130 - Science at the nanoscale

8:11
RPS: PSP0007 - Science-at-Nanoscale
June 9, 2009
Low-Dimensional Nanostructures
120
States
of
Density
A A
B B
2
0
-2
energy (eV)
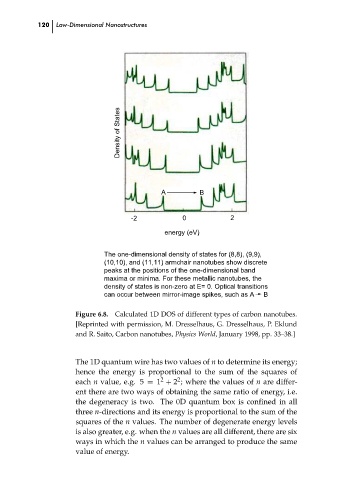
The one-dimensional density of states for (8,8), (9,9),
(10,10), and (11,11) armchair nanotubes show discrete
peaks at the positions of the one-dimensional band
maxima or minima. For these metallic nanotubes, the
density of states is non-zero at E= 0. Optical transitions
can occur between mirror-image spikes, such as A
B
Figure 6.8. Calculated 1D DOS of different types of carbon nanotubes.
[Reprinted with permission, M. Dresselhaus, G. Dresselhaus, P. Eklund
and R. Saito, Carbon nanotubes, Physics World, January 1998, pp. 33–38.] ch06
The 1D quantum wire has two values of n to determine its energy;
hence the energy is proportional to the sum of the squares of
2
2
each n value, e.g. 5 = 1 + 2 ; where the values of n are differ-
ent there are two ways of obtaining the same ratio of energy, i.e.
the degeneracy is two. The 0D quantum box is confined in all
three n-directions and its energy is proportional to the sum of the
squares of the n values. The number of degenerate energy levels
is also greater, e.g. when the n values are all different, there are six
ways in which the n values can be arranged to produce the same
value of energy.