Page 51 - Science at the nanoscale

RPS: PSP0007 - Science-at-Nanoscale
9:2
June 9, 2009
3.2. Basic Postulates of Quantum Mechanics
E4=16E1
n=4
n=3
E3=9E1
E2=4E1
n=2
E1
n=1
ȌQ [
_ȌQ [ _
2
Energy
Quantum
Number
Levels
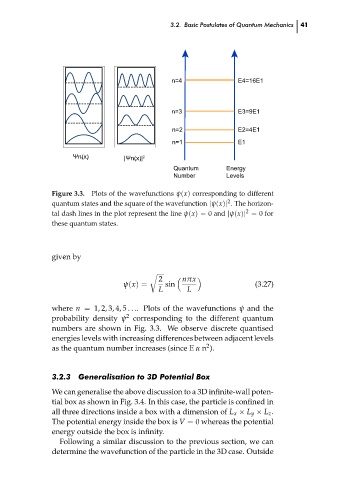
Plots of the wavefunctions ψ(x) corresponding to different
Figure 3.3.
2
quantum states and the square of the wavefunction |ψ(x)| . The horizon-
2
tal dash lines in the plot represent the line ψ(x) = 0 and |ψ(x)| = 0 for
these quantum states.
given by
r
nπx
2

(3.27)
sin
ψ(x) =
L
L
where n = 1, 2, 3, 4, 5 . . .. Plots of the wavefunctions ψ and the
2
probability density ψ corresponding to the different quantum
numbers are shown in Fig. 3.3. We observe discrete quantised
energies levels with increasing differences between adjacent levels 41 ch03
2
as the quantum number increases (since E α n ).
3.2.3 Generalisation to 3D Potential Box
We can generalise the above discussion to a 3D infinite-wall poten-
tial box as shown in Fig. 3.4. In this case, the particle is confined in
all three directions inside a box with a dimension of L x × L y × L z .
The potential energy inside the box is V = 0 whereas the potential
energy outside the box is infinity.
Following a similar discussion to the previous section, we can
determine the wavefunction of the particle in the 3D case. Outside