Page 554 - Sensors and Control Systems in Manufacturing

SpectRx NIR Technology
On the other hand, if B(σ) has features much narrower than the ILS, 507
S observed (σ) will be greatly affected by the response of the system. This
is often referred to as under-resolving. In this case, the narrow lines
from B(σ) would all have widths very similar to that of the ILS. In the
limiting case of an isolated monochromatic line, the measured spec-
trum is the ILS itself, as illustrated in Fig. 10.10.
With respect to the instrument structure, many parameters influ-
ence the ILS, such as the finite mirror scan length, the finite diver-
gence in the interferometer, the IR alignment, and so on.

10.8.1 Spectral Resolution
In the present system, the width of the ILS is mainly governed by the
extent of the finite length of the interferogram. For a system with neg-
ligible divergence that is equipped with a round detector, the normal-
ized ILS is given by:

′
ILS(, ) =σσ Sin ( πσ2 MPD) (10.33)
2 πσ MPD

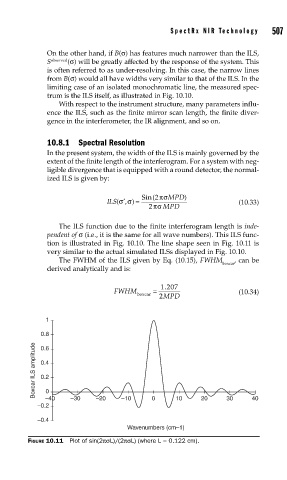
The ILS function due to the finite interferogram length is inde-
pendent of σ (i.e., it is the same for all wave numbers). This ILS func-
tion is illustrated in Fig. 10.10. The line shape seen in Fig. 10.11 is
very similar to the actual simulated ILSs displayed in Fig. 10.10.
The FWHM of the ILS given by Eq. (10.15), FWHM , can be
boxcar
derived analytically and is:
.
FWHM boxcar = 1 207 (10.34)
2 MPD

1
0.8
Boxcar ILS amplitude 0.4
0.6

0.2
0
–40
–0.2 –30 –20 –10 0 10 20 30 40
–0.4
Wavenumbers (cm–1)

FIGURE 10.11 Plot of sin(2πσL)/(2πσL) (where L = 0.122 cm).