Page 154 - Six Sigma Demystified

Chapter 6 a n a ly z e S tag e 135

the necessary combinations of factors, randomized to remove bias from main
effects. The data may not include sufficient variation in each factor or interac-
tion to statistically estimate a significance of the parameter. The uncontrolled
nature of the data collection may allow other factors (often unrecorded) to
contribute to noise in the data that may cloud the effects of each factor or be
confounded with factors that seem important (as described at the end of the
preceding section). Since the data are not run in random order, it is possible for
unrecognized factors that vary over time to bias the results.
ANOVA may be applied to the results of the designed experiment to deter-
mine the significance of factors. In this way, a seemingly complex process with
many variables can be reduced to only its few significant factors. Regression
analysis will be used to construct an equation for predicting the response given
the settings of the significant process factors (defined by the ANOVA).
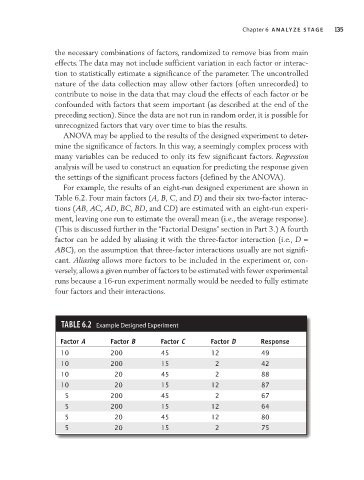
For example, the results of an eight- run designed experiment are shown in
Table 6.2. Four main factors (A, B, C, and D) and their six two- factor interac-
tions (AB, AC, AD, BC, BD, and CD) are estimated with an eight- run experi-
ment, leaving one run to estimate the overall mean (i.e., the average response).
(This is discussed further in the “Factorial Designs” section in Part 3.) A fourth
factor can be added by aliasing it with the three- factor interaction (i.e., D =
ABC), on the assumption that three- factor interactions usually are not signifi-
cant. Aliasing allows more factors to be included in the experiment or, con-
versely, allows a given number of factors to be estimated with fewer experimental
runs because a 16-run experiment normally would be needed to fully estimate
four factors and their interactions.

TAble­6.2­ Example Designed Experiment

Factor A Factor B Factor C Factor D Response
10 200 45 12 49
10 200 15 2 42
10 20 45 2 88
10 20 15 12 87
5 200 45 2 67
5 200 15 12 64
5 20 45 12 80
5 20 15 2 75