Page 147 - Statistics II for Dummies

Chapter 7: Getting Ahead of the Learning Curve with Nonlinear Regression 131

x
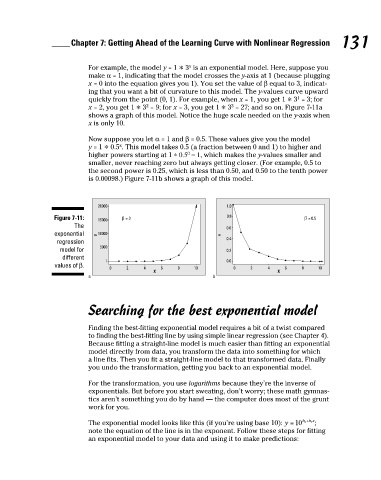
For example, the model y = 1 * 3 is an exponential model. Here, suppose you
make α = 1, indicating that the model crosses the y-axis at 1 (because plugging
x = 0 into the equation gives you 1). You set the value of β equal to 3, indicat-
ing that you want a bit of curvature to this model. The y-values curve upward
1
quickly from the point (0, 1). For example, when x = 1, you get 1 * 3 = 3; for
3
2
x = 2, you get 1 * 3 = 9; for x = 3, you get 1 * 3 = 27; and so on. Figure 7-11a
shows a graph of this model. Notice the huge scale needed on the y-axis when
x is only 10.
Now suppose you let α = 1 and β = 0.5. These values give you the model
x
y = 1 * 0.5 . This model takes 0.5 (a fraction between 0 and 1) to higher and
0
higher powers starting at 1 ∗ 0.5 = 1, which makes the y-values smaller and
smaller, never reaching zero but always getting closer. (For example, 0.5 to
the second power is 0.25, which is less than 0.50, and 0.50 to the tenth power
is 0.00098.) Figure 7-11b shows a graph of this model.

20000 1.0
Figure 7-11: 15000 0.8
The 0.6
exponential Y 10000 Y
0.4
regression
5000
model for 0.2
different
1 0.0
values of β.
0 2 4 6 8 10 0 2 4 6 8 10
X X
a b

Searching for the best exponential model

Finding the best-fitting exponential model requires a bit of a twist compared
to finding the best-fitting line by using simple linear regression (see Chapter 4).
Because fitting a straight-line model is much easier than fitting an exponential
model directly from data, you transform the data into something for which
a line fits. Then you fit a straight-line model to that transformed data. Finally
you undo the transformation, getting you back to an exponential model.

For the transformation, you use logarithms because they’re the inverse of
exponentials. But before you start sweating, don’t worry; these math gymnas-
tics aren’t something you do by hand — the computer does most of the grunt
work for you.

The exponential model looks like this (if you’re using base 10): ;
note the equation of the line is in the exponent. Follow these steps for fitting
an exponential model to your data and using it to make predictions:

12_466469-ch07.indd 131 7/24/09 9:39:10 AM