Page 93 - Statistics and Data Analysis in Geology

Analysis of Sequences of Data
‘I

8
lo] 0

d a 0
2 4 0 . 0
0
24 @ O
0. 0 . a
0 I ~ , I J I ~ I I I I ~ I I I J ~ I I I l

10-

8-
0 0
5 n-
6-’
0
z 4-
00 0000
00
2- ooooo
00 ooooo b
0 I I I I I I I 0 I I I I I I I I I I I I I l l I
Distance, m

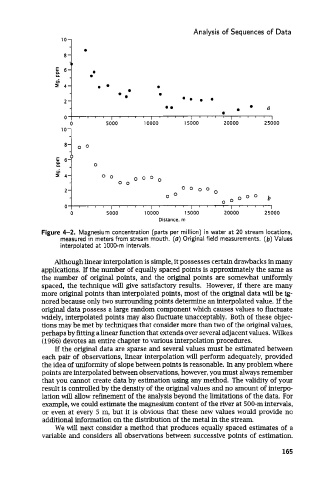
Figure 4-2. Magnesium concentration (parts per million) in water at 20 stream locations,
measured in meters from stream mouth. (a) Original field measurements. (b) Values
interpolated at 1000-m intervals.

Although linear interpolation is simple, it possesses certain drawbacks in many
applications. If the number of equally spaced points is approximately the same as
the number of original points, and the original points are somewhat uniformly
spaced, the technique will give satisfactory results. However, if there are many
more original points than interpolated points, most of the original data will be ig-
nored because only two surrounding points determine an interpolated value. If the
original data possess a large random component which causes values to fluctuate
widely, interpolated points may also fluctuate unacceptably. Both of these objec-
tions may be met by techniques that consider more than two of the original values,
perhaps by fitting a linear function that extends over several adjacent values. Wilkes
(1966) devotes an entire chapter to various interpolation procedures.
If the original data are sparse and several values must be estimated between
each pair of observations, linear interpolation will perform adequately, provided
the idea of uniformity of slope between points is reasonable. In any problem where
points are interpolated between observations, however, you must always remember
that you cannot create data by estimation using any method. The validity of your
result is controlled by the density of the original values and no amount of interpo-
lation will allow refinement of the analysis beyond the limitations of the data. For
example, we could estimate the magnesium content of the river at 500-m intervals,
or even at every 5 m, but it is obvious that these new values would provide no
additional information on the distribution of the metal in the stream.
We will next consider a method that produces equally spaced estimates of a
variable and considers all observations between successive points of estimation.

165