Page 94 - Statistics and Data Analysis in Geology

Statistics and Data Analysis in Geology - Chapter 4

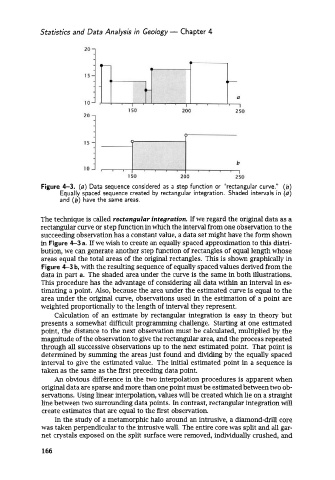
Figure 4-3. (a) Data sequence considered as a step function or "rectangular curve." (b)
Equally spaced sequence created by rectangular integration. Shaded intervals in (a)
and (b) have the same areas.

The technique is called rectangular integration. If we regard the original data as a
rectangular curve or step function in which the interval from one observation to the
succeeding observation has a constant value, a data set might have the form shown
in Figure 4-3 a. If we wish to create an equally spaced approximation to this distri-
bution, we can generate another step function of rectangles of equal length whose
areas equal the total areas of the original rectangles. This is shown graphically in
Figure 4-3 b, with the resulting sequence of equally spaced values derived from the
data in part a. The shaded area under the curve is the same in both illustrations.
This procedure has the advantage of considering all data within an interval in es-
timating a point. Also, because the area under the estimated curve is equal to the
area under the original curve, observations used in the estimation of a point are
weighted proportionally to the length of interval they represent.
Calculation of an estimate by rectangular integration is easy in theory but
presents a somewhat difficult programming challenge. Starting at one estimated
point, the distance to the next observation must be calculated, multiplied by the
magnitude of the observation to give the rectangular area, and the process repeated
through all successive observations up to the next estimated point. That point is
determined by summing the areas just found and dividing by the equally spaced
interval to give the estimated value. The initial estimated point in a sequence is
taken as the same as the first preceding data point.
An obvious difference in the two interpolation procedures is apparent when
original data are sparse and more than one point must be estimated between two ob-
servations. Using linear interpolation, values will be created which lie on a straight
line between two surrounding data points. In contrast, rectangular integration will
create estimates that are equal to the first observation.
In the study of a metamorphic halo around an intrusive, a diamond-drill core
was taken perpendicular to the intrusive wall. The entire core was split and all gar-
net crystals exposed on the split surface were removed, individually crushed, and

166