Page 352 - The Mechatronics Handbook

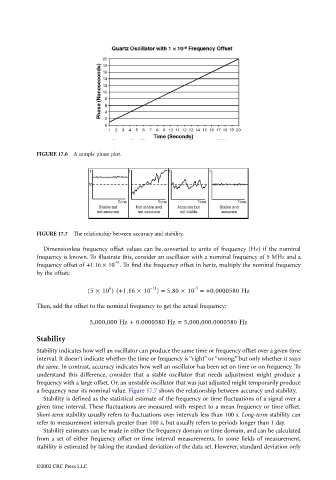
FIGURE 17.6 A sample phase plot.

FIGURE 17.7 The relationship between accuracy and stability.

Dimensionless frequency offset values can be converted to units of frequency (Hz) if the nominal
frequency is known. To illustrate this, consider an oscillator with a nominal frequency of 5 MHz and a
-11
frequency offset of +1.16 × 10 . To find the frequency offset in hertz, multiply the nominal frequency
by the offset:

-5
-11
6
(5 × 10 ) (+1.16 × 10 ) = 5.80 × 10 = +0.0000580 Hz
Then, add the offset to the nominal frequency to get the actual frequency:
5,000,000 Hz + 0.0000580 Hz = 5,000,000.0000580 Hz

Stability
Stability indicates how well an oscillator can produce the same time or frequency offset over a given time
interval. It doesn’t indicate whether the time or frequency is “right” or “wrong,” but only whether it stays
the same. In contrast, accuracy indicates how well an oscillator has been set on time or on frequency. To
understand this difference, consider that a stable oscillator that needs adjustment might produce a
frequency with a large offset. Or, an unstable oscillator that was just adjusted might temporarily produce
a frequency near its nominal value. Figure 17.7 shows the relationship between accuracy and stability.
Stability is defined as the statistical estimate of the frequency or time fluctuations of a signal over a
given time interval. These fluctuations are measured with respect to a mean frequency or time offset.
Short-term stability usually refers to fluctuations over intervals less than 100 s. Long-term stability can
refer to measurement intervals greater than 100 s, but usually refers to periods longer than 1 day.
Stability estimates can be made in either the frequency domain or time domain, and can be calculated
from a set of either frequency offset or time interval measurements. In some fields of measurement,
stability is estimated by taking the standard deviation of the data set. However, standard deviation only

©2002 CRC Press LLC