Page 761 - The Mechatronics Handbook

0066_Frame_C24 Page 9 Thursday, January 10, 2002 3:43 PM

Structure of the Unforced Response
In the absence of input, the state evolves as a combination of natural modes which belong to a defined
class of functions: all those generated by exponentials with either real or complex exponents. Hence these
modes include constants, real exponentials, pure sine waves, exponentially modulated sine waves, and
some other specials functions arising from repeated eigenvalues.
To illustrate these ideas and their physical interpretation consider the system in Example 24.1. For that
system

0 1
A = (24.52)
K
D
– ----- – -----
M M
Hence, the system eigenvalues are solutions to the equation
K
2
det lIA) = l + D ----- = 0 (24.53)
(
----- l +
–
M M
i.e.,
2
D
D
K
l 1,2 = −-------- ± ---------- – ----- (24.54)
2M 4M 2 M
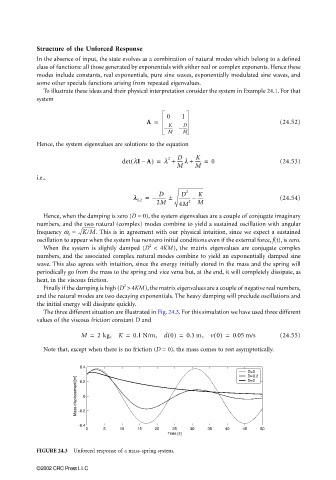
Hence, when the damping is zero (D = 0), the system eigenvalues are a couple of conjugate imaginary
numbers, and the two natural (complex) modes combine to yield a sustained oscillation with angular
frequency ω o = K/M . This is in agreement with our physical intuition, since we expect a sustained
oscillation to appear when the system has nonzero initial conditions even if the external force, f(t), is zero.
2
When the system is slightly damped (D < 4KM), the matrix eigenvalues are conjugate complex
numbers, and the associated complex natural modes combine to yield an exponentially damped sine
wave. This also agrees with intuition, since the energy initially stored in the mass and the spring will
periodically go from the mass to the spring and vice versa but, at the end, it will completely dissipate, as
heat, in the viscous friction.
2
Finally if the damping is high (D > 4KM), the matrix eigenvalues are a couple of negative real numbers,
and the natural modes are two decaying exponentials. The heavy damping will preclude oscillations and
the initial energy will dissipate quickly.
The three different situation are illustrated in Fig. 24.3. For this simulation we have used three different
values of the viscous friction constant D and
M = 2 kg, K = 0.1 N/m, d 0() = 0.3 m, v 0() = 0.05 m/s (24.55)

Note that, except when there is no friction (D = 0), the mass comes to rest asymptotically.

0.4
D=0
D=0.2
Mass displacement [m] -0.2 0
D=2
0.2

-0.4
0 5 10 15 20 25 30 35 40 45 50
Time [s]
FIGURE 24.3 Unforced response of a mass-spring system.

©2002 CRC Press LLC