Page 859 - The Mechatronics Handbook

0066_frame_C27 Page 20 Friday, January 18, 2002 5:45 PM

The phase margin occurs at the gain crossover frequency ω c when |G(jω c )| = 1, or

2
------------------------------------------- = 1
ω n
2 1/2
(
ω c ω c + 4ς ω n )
2
2
This equation can be rewritten as
2 2
( ω c ) + 4ς ω n ω c ) ω n = 0
2
2
2
4
(
–
Solving for positive ω c , we obtain
2
------ = ( 4ς + 1) 1/2 – 2ς 2
4
ω c
2
ω n
Substituting s = jω c into Eq. (27.15), the phase margin for the system is
PM = 180° + ∠ Gjω c )
(
ω c 
= 180° 90° tan – 1   ------------ 
–
–
2ςω n
1 1
2 1/2
= 90° tan –   ----- 4ς +([ 4 1) 1/2 – 2ς ]  
–
2ς
 1/2 
1
= tan  2ς -----------------------------------------  (27.16)
1
–
 ( 4ς + 1) 1/2 – 2ς 2 
4
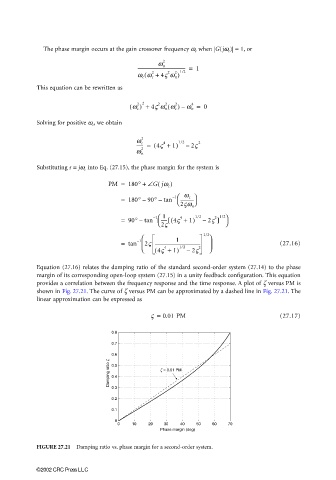
Equation (27.16) relates the damping ratio of the standard second-order system (27.14) to the phase
margin of its corresponding open-loop system (27.15) in a unity feedback configuration. This equation
provides a correlation between the frequency response and the time response. A plot of ζ versus PM is
shown in Fig. 27.21. The curve of ζ versus PM can be approximated by a dashed line in Fig. 27.21. The
linear approximation can be expressed as
ς = 0.01 PM (27.17)
0.8
0.7
0.6
Damping ratio z 0.5 z = 0.01 PM

0.4
0.3
0.2
0.1
0
0 10 20 30 40 50 60 70
Phase margin (deg)

FIGURE 27.21 Damping ratio vs. phase margin for a second-order system.

©2002 CRC Press LLC