Page 997 - The Mechatronics Handbook

0066_frame_Ch33.fm Page 21 Wednesday, January 9, 2002 8:00 PM

TABLE 33.1
Regulator IAE ISE
PID (chapter 4) 0.8042 3.4754
PI (chapter 4) 0.8006 3.4618
PD (chapter 4) 0.7928 3.4537
Neural (chapter 6) 0.8027 3.4622
Neuro-fuzzy (chapter 7) 0.7911 3.4501

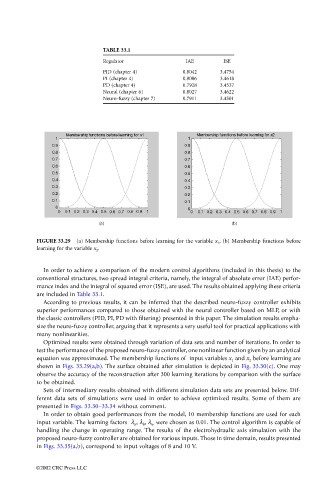
FIGURE 33.29 (a) Membership functions before learning for the variable x 1 , (b) Membership functions before
learning for the variable x 2 .

In order to achieve a comparison of the modern control algorithms (included in this thesis) to the
conventional structures, two spread integral criteria, namely, the integral of absolute error (IAE) perfor-
mance index and the integral of squared error (ISE), are used. The results obtained applying these criteria
are included in Table 33.1.
According to previous results, it can be inferred that the described neuro-fuzzy controller exhibits
superior performances compared to those obtained with the neural controller based on MLP, or with
the classic controllers (PID, PI, PD with filtering) presented in this paper. The simulation results empha-
size the neuro-fuzzy controller, arguing that it represents a very useful tool for practical applications with
many nonlinearities.
Optimized results were obtained through variation of data sets and number of iterations. In order to
test the performance of the proposed neuro-fuzzy controller, one nonlinear function given by an analytical
equation was approximated. The membership functions of input variables x 1 and x 2 before learning are
shown in Figs. 33.29(a,b). The surface obtained after simulation is depicted in Fig. 33.30(c). One may
observe the accuracy of the reconstruction after 300 learning iterations by comparison with the surface
to be obtained.
Sets of intermediary results obtained with different simulation data sets are presented below. Dif-
ferent data sets of simulations were used in order to achieve optimized results. Some of them are
presented in Figs. 33.30–33.34 without comment.
In order to obtain good performances from the model, 10 membership functions are used for each
input variable. The learning factors λ a , λ b , λ w were chosen as 0.01. The control algorithm is capable of
handling the change in operating range. The results of the electrohydraulic axis simulation with the
proposed neuro-fuzzy controller are obtained for various inputs. Those in time domain, results presented
in Figs. 33.35(a,b), correspond to input voltages of 8 and 10 V.

©2002 CRC Press LLC