Page 79 - Theory and Design of Air Cushion Craft

Practical formulae for predicting air cushion performance 63

0.75 -

0.50 -

0.5 1.0 1.5 2.0 hit
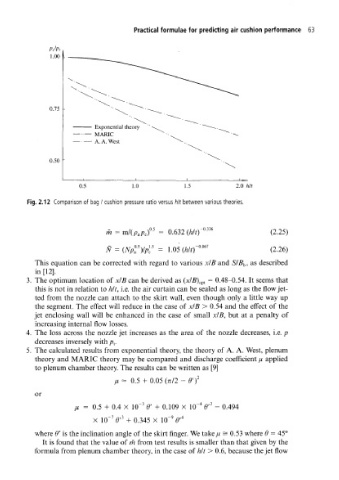
Fig. 2.12 Comparison of bag / cushion pressure ratio versus hit between various theories.

m = m/(/? a/7 c) 05 = 0.632 (h/t)~°' m (2.25)
nc -0.067
t (2.26)
= 1-05
This equation can be corrected with regard to various xlB and S75 b, as described
in [12].
3. The optimum location of xlB can be derived as (x/B) opt = 0.48-0.54. It seems that
this is not in relation to hit, i.e. the air curtain can be sealed as long as the flow jet-
ted from the nozzle can attach to the skirt wall, even though only a little way up
the segment. The effect will reduce in the case of xlB > 0.54 and the effect of the
jet enclosing wall will be enhanced in the case of small x/B, but at a penalty of
increasing internal flow losses.
4. The loss across the nozzle jet increases as the area of the nozzle decreases, i.e. p
decreases inversely with p t.
5. The calculated results from exponential theory, the theory of A. A. West, plenum
theory and MARIC theory may be compared and discharge coefficient ju applied
to plenum chamber theory. The results can be written as [9]
0.5 + 0.05 (Ti/2 - <9')
or
4
li = 0.5 + 0.4 X 10~ 3 9' + 0.109 X 10" 9' 2 - 0.494
7
X 10~ 6>' 3 + 0.345 X 10~V 4
where 0' is the inclination angle of the skirt finger. We take/z = 0.53 where 9 = 45°
It is found that the value of m from test results is smaller than that given by the
formula from plenum chamber theory, in the case of hit > 0.6, because the jet flow