Page 453 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)
P. 453
440 Random Vibrations Chap. 13
x{f) i p(^)
H_____
Ww||wyp f if 'n F i
2.0
0 ------------ 1------- r
I 1 ' '
Figure 13.6-8.
Example 13.6-2
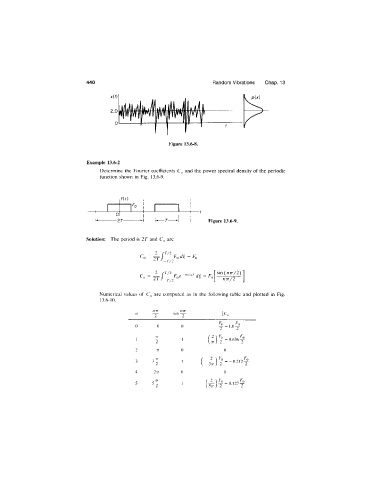
Determine the Fourier coefficients C„ and the power spectral density of the periodic
function shown in Fig. 13.6-9.
MM 1
rr 1 1
1 ^0 ! 1
1 1 ___ 1_
1 0 j 1
[------------- 2 T------ L— r — Figure 13.6-9.
Solution: The period is 2T and C„ are
C = r^/2 f = f
-T /2
sin {mr/2)
mr/2
Numerical values of Q are computed as in the following table and plotted in Fig.
13.6-10.
riTT /177
n Sin - r
2 ^ t
~ Y
Fn
0 0 0 1 . 0 ^
2
77
1 1 (§: 0 .6 3 6 ^
2
2 77 0 0
T - 1 T()
3 - 0 . 2 1 2 ^
4 2 t7 0 0
To
5 1 (è; 0 .1 2 7 ^