Page 449 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

436 Random Vibrations Chap. 13

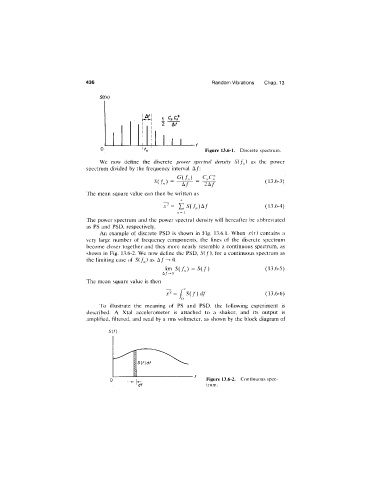
S(fn)

Figure 13.6-1. Discrete spectrum.
We now define the discrete power spectral density S(f^) as the power
spectrum divided by the frequency interval A/:
G (/„ ) c „ c
S{fn) = (13.6-3)

The mean square value can then be written as
00
(13.6-4)
1
The power spectrum and the power spectral density will hereafter be abbreviated
as PS and PSD, respectively.
An example of discrete PSD is shown in Fig. 13.6.1. When x{t) contains a
very large number of frequency components, the lines of the discrete spectrum
become closer together and they more nearly resemble a continuous spectrum, as
shown in Fig. 13.6-2. We now define the PSD, A(/), for a continuous spectrum as
the limiting case of S(f^) as A / ^ 0.
lim S { f „ ) =S ( f ) (13.6-5)
A/^0
The mean square value is then
r s ( f ) d f (13.6-6)
•'n
To illustrate the meaning of PS and PSD, the following experiment is
described. A Xtal accelerometer is attached to a shaker, and its output is
amplified, filtered, and read by a rms voltmeter, as shown by the block diagram of

S{f)

Figure 13.6-2. Continuous spec­
trum.