Page 451 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)
P. 451
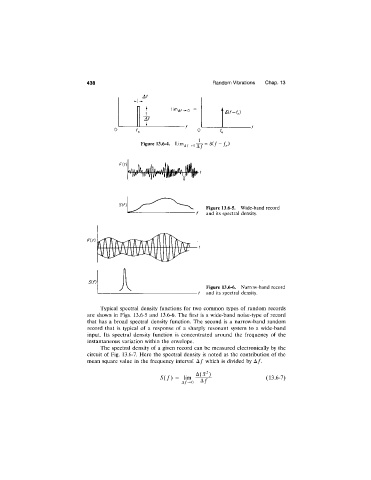
438 Random Vibrations Chap. 13
k -
k
1 ¿(f-Q
Af
1
Figure 13.6-4. = 0 ( / - / „ )
F{t)
Sin
Figure 13.6-5. Wide-band record
f and its spectral density.
Figure 13.6-6. Narrow-band record
-f and its spectral density.
Typical spectral density functions for two common types of random records
are shown in Figs. 13.6-5 and 13.6-6. The first is a wide-band noise-type of record
that has a broad spectral density function. The second is a narrow-band random
record that is typical of a response of a sharply resonant system to a wide-band
input. Its spectral density function is concentrated around the frequency of the
instantaneous variation within the envelope.
The spectral density of a given record can be measured electronically by the
circuit of Fig. 13.6-7. Here the spectral density is noted as the contribution of the
mean square value in the frequency interval A / which is divided by A/.
S( f ) = lim A m (13.6-7)
A/^O A/