Page 14 - Thermodynamics of Biochemical Reactions

1.3 Binding of Hydrogen Ions and Magnesium Ions by Adenosine Triphosphate 7

Table 1.2 Equilibrium Constants in the ATP Series at 298.15 K

Reaction pK(I=0) K(I=0) K(I=0.25 M)
~- ~ ~ ~~ ~~
HAMP-= H+ + AMP2- 6.73 1.862 x 6.877 x
H2AMP = H+ + HAMP- 3.99 1.023 x 1.966 x
MgAMP = Mg2+ + AMP2 2.79 1.622 x 2.212 x lo-,
HADP2- = H+ + ADP-3 KI,,, 7.18 6.607 x lo-' 4.689 x
H2ADP ~- = H + + HADP' K2ADP 4'36 4.365 x 10-j 1.612 x
MgADP- = Mg2+ + ADP3- K3,DP 4.65 2.239 x 10-5 1.128 x
MgHADP = Mg2' + HADP2- K,,,, 2.50 3.162 x 4.313 x
HATP3- = H+ + ATP4- KiATP 7.60 2.512 x lo-* 3.426 x
H,ATP~- = H+ + HATP" K,,,, 4.68 2.089 x 10-5 1.483 x
MgATP2- = Mg2+ + ATP4- KMTP 6.18 6.607 x 1.229 x lo-,
MgHATP- = Mg2+ + HATP3 K,,,, 3.63 2.344 x 1.181 x
Mg2ATP = Mg2+ + MgATP2- K,,,, 2.69 2.042 x 2.785 x 1 -'
H,PO, = H+ + HP0:- 7.22 6.026 x lo-' 2.225 x lo-'
MgHPO, = Mg2+ + HPO;- 2.71 1.950 x 2.66 x
HG6P- = H+ + G6P2- 6.42 3.802 x 1.404 x
MgG6P = Mgzi + G6P2- 2.60 2.512 x 3.462 x lo-'
Hadenosine' = H+ + adenosine 3.50 3.162 x 3.162 x
ATP4- + H,O = ADP3- + HP0:- + H+ 2.946 x lo-'
ADP3-- + H,O = AMP2- + HP0;- + H+ 6.622 x lo-'
AMP2- + H,O = adenosine + HP0;- 1.894 x 10'
G6P2- + H,O = glucose + HP0;- 8.023 x 10'
ATP4- + glucose = ADP3- + G6P2- + H+ 3.671 x
2ADP3 = ATP4 + AMP2 2.248 x lo-'

Source: R. A. Alberty and R. N. Goldberg, Biochem., 31, 10612 (1992). Copyright 1992 American
Chemical Society.

r(H2ATP2-) = KIATI'KZATP (1.3-5)

KZATP
These mole fractions are plotted versus pH at 298.15 K and I = 0.25 M in Fig. 1.2.
Since it is possible to calculate the mole fractions of the various species of
ATP at a specified pH, the average binding of hydrogen ions RH can be calculated
by use of
O[ATP4-] + 1[HATP3-] + 2[H,ATP2-]
NH = (1.3-6)
[ATPI

rr
-
_-
It _-- -

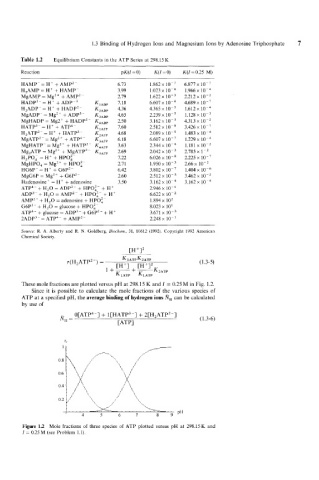
Figure 1.2 Mole fractions of three species of ATP plotted versus pH at 298.15K and
I = 0.25 M (see Problem 1.1).