Page 689 - Bird R.B. Transport phenomena

Problems 669

(b) Next use the equation of continuity for species A to obtain

(21B.2-2)
Sc ((
(0
{t)
in which Sc = /x /рЯЬ%. This equation is to be integrated with the boundary conditions that
U is finite at £ = 0 and dU x/d^ = 1 at f = \.
-
K
(c) Integrate once with respect to f to obtain
1/2
(v /{v )№
z
z
(21B.2-3)
fll
1
21B.3. An asymptotic expression for the turbulent mass flux. Start with the final result of Problem
21B.2, and note that for sufficiently high Sc all curvature of the concentration profile will take
place very near the wall, where /(v ) « 0 and £ « \. Assume that Sc (/) = 1 and use Eq. 5.4-2
v
z
z
to obtain
(21B.3-1)
(0
Sc(/i /At)]
1/3
Introduce the new coordinate rj = Sc (yi;*/14.5i>) into Eq. 21B.3-1 to get an equation for dU/dr)
valid within the laminar sublayer. Then integrate from 17 = 0 (where а> = ы ) to 17 = °° (where
л
А0
а> л ~ а) ) to obtain an explicit relation for the wall mass flux j . Compare with the analog of
л/7
A 0
Eq. 13.4-20 obtained in Problem 21 A.2.
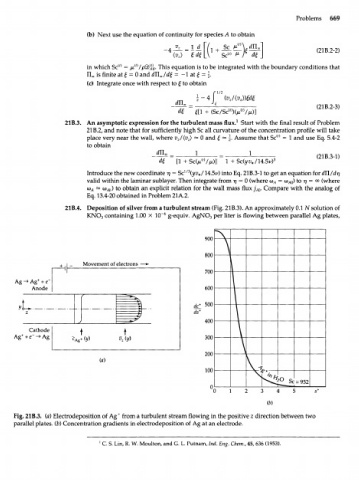
21B.4. Deposition of silver from a turbulent stream (Fig. 21B.3). An approximately 0.1 N solution of
KNO3 containing 1.00 X 10" 6 g-equiv. AgNO 3 per liter is flowing between parallel Ag plates,
900
800
Movement of electrons
700
Ag -> Ag + + e
Anode 600

500
ds +
400
Cathode
Ag + + e~ —> Ag 300 \

200 \
(a)
100
> о Sc = 952
л • • — —
°0 1i : > 3 L1 5 s +
(b)

Fig. 21B.3. (a) Electrodeposition of Ag + from a turbulent stream flowing in the positive z direction between two
parallel plates, (b) Concentration gradients in electrodeposition of Ag at an electrode.

1
С S. Lin, R. W. Moulton, and G. L. Putnam, Ind. Eng. Chetn., 45, 636 (1953).