Page 685 - Bird R.B. Transport phenomena

§21.5 Turbulent Mixing and Turbulent Flow with Second-Order Reaction 665

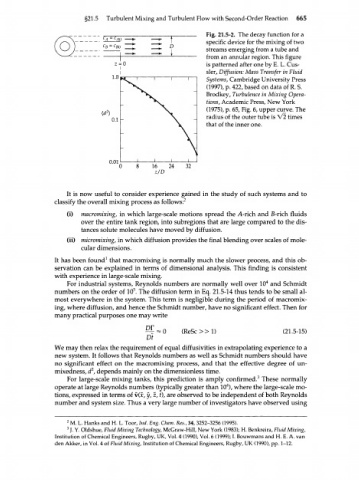
t Fig. 21.5-2. The decay function of for a
device
specific
two
the mixing
for
D
streams emerging from a tube and
from an annular region. This figure
is patterned after one by E. L. Cus-
sler, Diffusion: Mass Transfer in Fluid
Systems, Cambridge University Press
(1997), p. 422, based on data of R. S.
Brodkey, Turbulence in Mixing Opera-
tions, Academic Press, New York
(1975), p. 65, Fig. 6, upper curve. The
radius of the outer tube is V2 times
that of the inner one.

0.01
32

It is now useful to consider experience gained in the study of such systems and to
classify the overall mixing process as follows: 2

(i) macromixing, in which large-scale motions spread the Л-rich and B-rich fluids
over the entire tank region, into subregions that are large compared to the dis-
tances solute molecules have moved by diffusion.
(ii) micromixing, in which diffusion provides the final blending over scales of mole-
cular dimensions.
It has been found 1 that macromixing is normally much the slower process, and this ob-
servation can be explained in terms of dimensional analysis. This finding is consistent
with experience in large-scale mixing.
For industrial systems, Reynolds numbers are normally well over 10 4 and Schmidt
numbers on the order of 10\ The diffusion term in Eq. 21.5-14 thus tends to be small al-
most everywhere in the system. This term is negligible during the period of macromix-
ing, where diffusion, and hence the Schmidt number, have no significant effect. Then for
many practical purposes one may write

DT 0 (ReSc»l) (21.5-15)
Dt
We may then relax the requirement of equal diffusivities in extrapolating experience to a
new system. It follows that Reynolds numbers as well as Schmidt numbers should have
no significant effect on the macromixing process, and that the effective degree of un-
2
mixedness, d , depends mainly on the dimensionless time.
For large-scale mixing tanks, this prediction is amply confirmed. 3 These normally
4
operate at large Reynolds numbers (typically greater than 10 ), where the large-scale mo-
tions, expressed in terms of v(x, j/, z, t), are observed to be independent of both Reynolds
number and system size. Thus a very large number of investigators have observed using

2 M. L. Hanks and H. L. Toor, bid. Eng. Cliem. Res., 34, 3252-3256 (1995).
3
J. Y. Oldshue, Fluid Mixing Technology, McGraw-Hill, New York (1983); H. Benkreira, Fluid Mixing,
Institution of Chemical Engineers, Rugby, UK, Vol. 4 (1990), Vol. 6 (1999); I. Bouwmans and H. E. A. van
den Akker, in Vol. 4 of Fluid Mixing, Institution of Chemical Engineers, Rugby, UK (1990), pp. 1-12.