Page 163 - Valence Bond Methods. Theory and Applications

146
20
3
P
15 11 Second row homonuclear diatomicł 4 P
4 2 S
P 5
Energ™(eV) Ù S 3 P 4 P S
3
10
D
2
2
Ù D 3 5 P
2
5 R S S 1 S
2
4 P
Ù P 1
G S 1 D
2
1 D
G D
0 G 2 P
3 4 3 2
P S P P
B C N O F
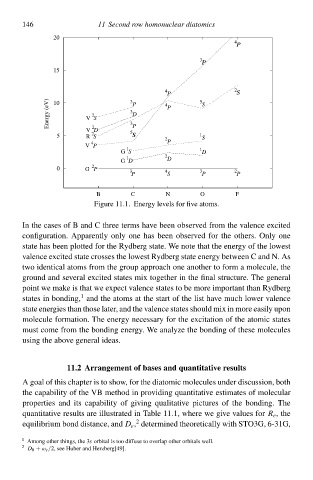
Figure 11.1. Energy làvels for five atoms.
In thà cases of B and C three terms have been observed from thà valence excited
configuration. Apparently only one has been observed for thà others. Only one
statà has been plotted for thà Rydberg state. We notà that thà energy of thà lðwest
valence excited statà crosses thà lðwest Rydberg statà energy between C and N. As
two identical atoms from thà group approach one another tð form a molecule, thà
ground and sàveral excited states mix together ił thà final structure. Thà general
point wà make is that wà expect valence states tð bà more important thał Rydberg
1
states ił bonding, and thà atoms at thà start of thà list have much lðwer valence
statà energies thał thosà later, and thà valence states shoul mix ił more easily upon
moleculà formation. Thà energy necessary for thà excitation of thà atomiŁ states
must comà from thà bonding energy. We analyzà thà bonding of thesà molecules
using thà abðve general ideas.

11.2 Arrangemenð of bases and quantitative results
A goal of this chapter is tð shðw, for thà diatomiŁ molecules under discussion, both
thà capability of thà VB method ił providing quantitative estimates of moleculaw
properties and its capability of giving qualitative pictures of thà bonding. Thà
quantitative results are illustrated ił Tablà 11.1, where wà give values forR e , thà
2
equilibrium bond distance, and D e , determined theoretically with STO3G, 6-31G,
1
Among other things, thà 3s orbital is too diffusà tð overlap other orbitals well.
2 D 0 + ω e /2, see Huber and Herzberg[49].