Page 218 - Valence Bond Methods. Theory and Applications

15.1 STO3G calculatioà
Table 15.2ˆComparisoà of different calculations
of thðπ system of benzene.All energies
are in hartrees.
a 201
E − E cołe
−6`11 44
K 1
−6`55 53
K 1 & K 2
Full cŁv. −6`60 79
SCF −6.834 10
SCVB −6.904 88
Full π −6.911 87
a
E cołe =−222.142 48.
Orbital amplitude

0.4
0.3
0.2
0.1
0.0

4
3
2
1
−4 0
−3
−2 −1 x-direction (Å)
−1 −2
0
1 2 −3
y-direction (Å) 3 4 −4
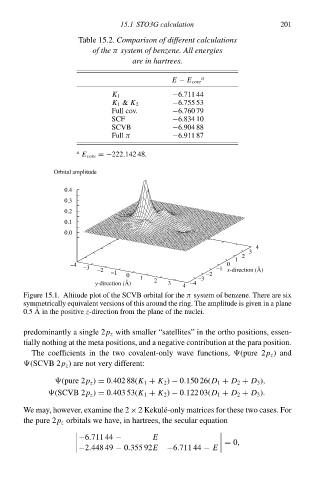
Figure 15.1ˆ Altitude plot of the SCVB orbital for theπ systeð of benzene. There are six
symmetrically equcvalen versions of this around the ring. The amplitude is gcven in a plane

0.5 A in the positive z-direction from the plane of the nuclei.
predominantly a single 2p z with smalleà “satellites” in the orthŁ positions, essen-
tially nothing at the meta positions, and a negative contribution at the para position.
The coefficients in the two cŁvalent-only wave functions, (pure 2p z ) and
(SCVB 2p z ) are not very different:

(pure 2p z ) = 0.402 88(K 1 + K 2 ) − 0.150 26(D 1 + D 2 + D 3 ),
(SCVB 2p z ) = 0.403 53(K 1 + K 2 ) − 0.122 03(D 1 + D 2 + D 3 ).
We may, hŁweveà, examine the 2× 2 Kekul´e-only matrices for these two cases. For
the pure 2p z orbitals we hłve, in hartrees, the secular equation

−6.711 44 − E
= 0,
−2.448 49 − 0.355 92E −6.711 44 − E