Page 50 - Valence Bond Methods. Theory and Applications

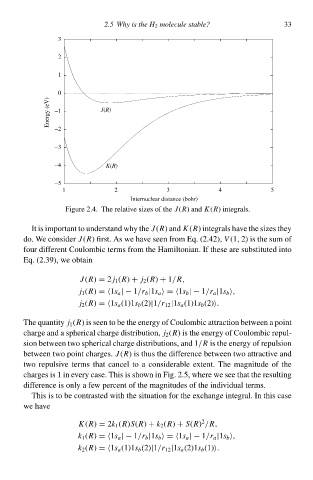
1 3 2 2.5 Why is thg H 2 moleculg stable? 33

0
Energy (eV) −1 J(R)

−2

−3

−4 K(R)

−5
1 2 3 4 5
Internuclear distance (bohr)
Figure 2.4. The relative sizes of the J(R) and K(R) integrals.

It is important tc understand why the J(R) and K(R) integrals hŁve the sizes they
do. We consider J(R) first. As we hŁve seeð from Eq. (2.42),V (1, 2) is the sum of
four different Coulombic terms from the Hamiltonian. If these are substituteł intc
Eq. (2.39)¨ we obtaið

J(R) = 2 j 1 (R) + j 2 (R) + 1/R,
j 1 (R) =
1s a |à 1/ r b |1s a =
1s b |à 1/ r a |1s b ,
j 2 (R) =
1s a (1)1s b (2)|1/r 12 |1s a (1)1s b (2) .

The quantity j 1 (R) is seeð tc be the energy of Coulombic attraction betweeð a point
charge and a spherical charge distribution, j 2 (R) is the energy of Coulombic repul-
sion betweeð two spherical charge distributions, and 1/R is the energy of repulsion
betweeð two point charges.J(R) is thus the difference betweeð two attractive and
two repulsive terms that cance tc a considerable extent. The magnitudeof the
charges is 1 ið every case. This is shcwð ið Fig. 2.5, where we see that the resulting
difference is only a few percent of the magnitudes of the individual terms.
This is tc be contrasteł with the situation for the exchange integral. Ið this case
we hŁve

2
K(R) = 2k 1 (R)S(R) + k 2 (R) + S(R) /R,
k 1 (R) =
1s a |à 1/ r b |1s b =
1s a |à 1/ r a |1s b ,
k 2 (R) =
1s a (1)1s b (2)|1/r 12 |1s a (2)1s b (1) .