Page 106 - Wind Energy Handbook

80 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

2
äC P ¼ 8ìa(1 a) äì (3:72)

Whereas, from the Kutta–Joukowski theorem, the circulation ˆ on the blade, which
is uniform, provides a torque per unit span of

äQ
¼ r(W 3 ˆ)sin ö r r
är
where the angle ö r is determined by the flow velocity local to the blade.
The strength of the total circulation for all three blades is given by Equation (3.65)
and so, in the presence of tip-loss the increment of power coefficient from a blade
element is
äC P ¼ 8ìa(1 a)(1 a r )äì (3:73)

where a ¼ 1=3 is the average axial flow induction factor and a r is the value local to
the blade.
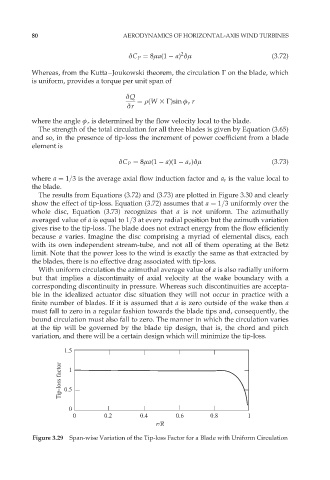
The results from Equations (3.72) and (3.73) are plotted in Figure 3.30 and clearly
show the effect of tip-loss. Equation (3.72) assumes that a ¼ 1=3 uniformly over the
whole disc, Equation (3.73) recognizes that a is not uniform. The azimuthally
averaged value of a is equal to 1=3 at every radial position but the azimuth variation
gives rise to the tip-loss. The blade does not extract energy from the flow efficiently
because a varies. Imagine the disc comprising a myriad of elemental discs, each
with its own independent stream-tube, and not all of them operating at the Betz
limit. Note that the power loss to the wind is exactly the same as that extracted by
the blades, there is no effective drag associated with tip-loss.
With uniform circulation the azimuthal average value of a is also radially uniform
but that implies a discontinuity of axial velocity at the wake boundary with a
corresponding discontinuity in pressure. Whereas such discontinuities are accepta-
ble in the idealized actuator disc situation they will not occur in practice with a
finite number of blades. If it is assumed that a is zero outside of the wake then a
must fall to zero in a regular fashion towards the blade tips and, consequently, the
bound circulation must also fall to zero. The manner in which the circulation varies
at the tip will be governed by the blade tip design, that is, the chord and pitch
variation, and there will be a certain design which will minimize the tip-loss.

1.5
Tip-loss factor 0.5
1

0
0 0.2 0.4 0.6 0.8 1
r/R
Figure 3.29 Span-wise Variation of the Tip-loss Factor for a Blade with Uniform Circulation