Page 110 - Wind Energy Handbook

84 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

effect upon the wake flow. The theory applies only to the developed wake. In order
to simplify his analysis Prandtl replaced the helicoidal sheets with a succession of
discs, moving with the uniform, central wake velocity U 1 (1 a) and separated by
the same distance as the normal distance between the vortex sheets. Conceptually,
the discs, travelling axially with velocity U 1 (1 a) would encounter the unattenu-
ated free-stream velocity U 1 at their outer edges. The fast flowing free-stream air
would tend to weave in and out between successive discs. The wider apart
successive discs the deeper, radially, the free-stream air would penetrate. Taking
any line parallel to the rotor axis at a radius r, somewhat smaller than the wake
radius (rotor radius), the average axial velocity along that line would be greater
than U 1 (1 a) and less than U 1 . Let the average velocity be U 1 (1 af(r)), where
f(r) is the tip-loss function, has a value less than unity and falls to zero at the wake
boundary. At a distance from the wake edge the free-stream fails to penetrate and
there is little or no difference between the induced velocity at the blade and that in
the wake, i.e., f(r) ¼ 1.
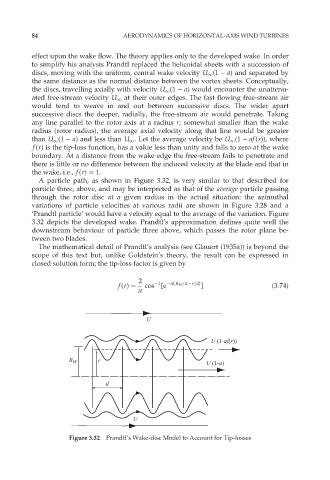
A particle path, as shown in Figure 3.32, is very similar to that described for
particle three, above, and may be interpreted as that of the average particle passing
through the rotor disc at a given radius in the actual situation: the azimuthal
variations of particle velocities at various radii are shown in Figure 3.28 and a
‘Prandtl particle’ would have a velocity equal to the average of the variation. Figure
3.32 depicts the developed wake. Prandtl’s approximation defines quite well the
downstream behaviour of particle three above, which passes the rotor plane be-
tween two blades.
The mathematical detail of Prandtl’s analysis (see Glauert (1935a)) is beyond the
scope of this text but, unlike Goldstein’s theory, the result can be expressed in
closed solution form; the tip-loss factor is given by

2
1
f(r) ¼ cos [e ð(R W =d r=d) ] (3:74)
ð

U

U (1-af(r))

R W r U (1-a)

d

U

Figure 3.32 Prandtl’s Wake-disc Model to Account for Tip-losses