Page 111 - Wind Energy Handbook

THE EFFECTS OF A DISCRETE NUMBER OF BLADES 85

R W r is a distance measured from the wake edge. Distance d between the discs
should be that of the distance travelled by particle three between successive vortex
sheets. Glauert (1935) takes d as being the normal distance between successive
helicoidcal vortex sheets.
The helix angle of the vortex sheets is the flow angle ö S and so with N sheets
intertwining from N blades

2ðR W 2ðR W U 1 (1 a)
d ¼ sin ö S ¼ (3:75)
N N W S
Prandtl’s model has no wake rotation but the discs may spin at the rotor speed
without affecting the flow at all, as it is inviscid, thus a9 is zero and W S is the
resultant velocity (not including the radial velocity) at the edge of a disc. Glauert
(1935a) argues that R W =W S r=W which is much more convenient to use.
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
W ¼ [U 1 (1 a)] þ (Ùr) 2
so
s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R W r N R r (Ùr) 2
ð ¼ 1 þ
r 2 d [U 1 (1 a)] 2
and

p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 2 2
f(ì) ¼ cos[e ((N=2)(1 ì)=ì) 1þ(ºì) =(1 a) ] (3:76)
ð
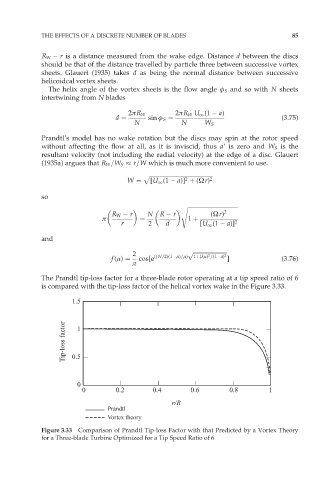
The Prandtl tip-loss factor for a three-blade rotor operating at a tip speed ratio of 6
is compared with the tip-loss factor of the helical vortex wake in the Figure 3.33.

1.5

Tip-loss factor 0.5
1

0
0 0.2 0.4 0.6 0.8 1
r/R
Prandtl
Vortex theory
Figure 3.33 Comparison of Prandtl Tip-loss Factor with that Predicted by a Vortex Theory
for a Three-blade Turbine Optimized for a Tip Speed Ratio of 6