Page 112 - Wind Energy Handbook

86 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

It should also be pointed out that the vortex theory of Figure 3.28 also predicts
that the tip-loss factor should be applied to the tangential flow induction factor.
It is now useful to know what is the variation of circulation along the blade. For
the previous analysis, which disregarded tip-losses, the blade circulation was
uniform (Equation (3.65)). Following the same procedure from which Equation
(3.64) was developed

U 3 1 2
r(W 3 ˆ)sin ö ¼ rˆU 1 (1 a b (r)) ¼ 4ðr a(r)(1 a(r))
Ù
Recall that a b (r) is the flow factor local to the blade at radius r, which is equal to a
and a(r) is the average value of the flow factor at radius r. Therefore

4ð U 2
ˆ(r) ¼ 1 af(r)(1 af(r)) 2 (3:77)
1 a Ù
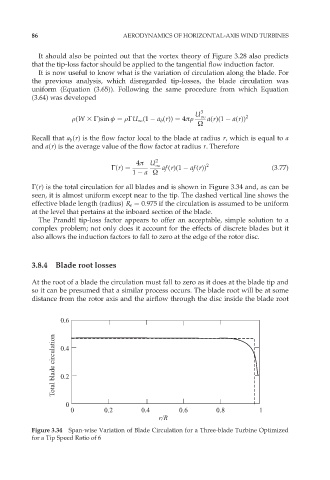
ˆ(r) is the total circulation for all blades and is shown in Figure 3.34 and, as can be
seen, it is almost uniform except near to the tip. The dashed vertical line shows the
effective blade length (radius) R e ¼ 0:975 if the circulation is assumed to be uniform
at the level that pertains at the inboard section of the blade.
The Prandtl tip-loss factor appears to offer an acceptable, simple solution to a
complex problem; not only does it account for the effects of discrete blades but it
also allows the induction factors to fall to zero at the edge of the rotor disc.

3.8.4 Blade root losses

At the root of a blade the circulation must fall to zero as it does at the blade tip and
so it can be presumed that a similar process occurs. The blade root will be at some
distance from the rotor axis and the airflow through the disc inside the blade root

0.6

Total blade circulation 0.4

0.2

0
0 0.2 0.4 0.6 0.8 1
r/R
Figure 3.34 Span-wise Variation of Blade Circulation for a Three-blade Turbine Optimized
for a Tip Speed Ratio of 6