Page 113 - Wind Energy Handbook

THE EFFECTS OF A DISCRETE NUMBER OF BLADES 87

radius will be at the free-stream velocity. Actually, the vortex theory of Section 3.4
can be extended to show that the flow through the root disc is somewhat higher
than the free-stream velocity. It is usual, therefore, to apply the Prandtl tip-loss
function at the blade root as well as at the tip.
If ì R is the normalized root radius then the root loss factor can be determined by
modifying the tip-loss factor of Equation (3.76).
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 N=2(ì ì R =ì) 1þ(ºì) =(1 a) 2
2
f R (ì) ¼ cos[e ] (3:78)
ð
If Equation (3.76) is now termed f T (r) the complete tip/root loss factor is

f(ì) ¼ f T (ì) f R (ì) (3:79)

3.8.5 Effect of tip-loss on optimum blade design and power

With no tip-loss the optimum axial flow induction factor is uniformly 1=3 over the
whole swept rotor. The presence of tip-loss changes the optimum value of the
average value of a which reduces to zero at the edge of the wake but, local to the
blade tends to increase in the tip region. If a(r) is taken as the azimuthal average at
radius r then locally, at the blade at that radius, the flow factor will be a(r)=f(r). The
inflow angle ö at the blade is then, from Equation (3.57),
0 a 1
1
1 B B f C C
tan ö ¼ B C (3:80)
ºì @ a9A
1 þ
f
but Equation (3.56), which is the ratio of the non-dimensional rate of change of

1.5
Tip/root-loss factor 0.5

1

0
0 0.2 0.4 0.6 0.8 1

r/R
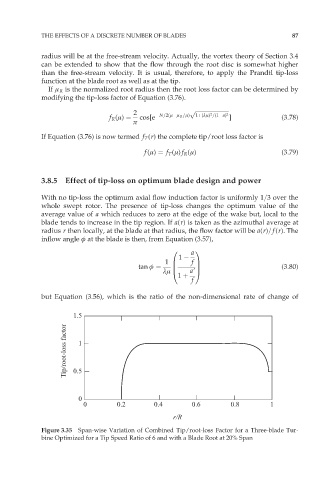
Figure 3.35 Span-wise Variation of Combined Tip/root-loss Factor for a Three-blade Tur-
bine Optimized for a Tip Speed Ratio of 6 and with a Blade Root at 20% Span