Page 420 - Wind Energy Handbook

394 COMPONENT DESIGN

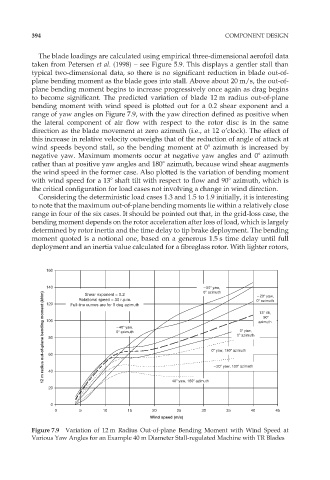
The blade loadings are calculated using empirical three-dimensional aerofoil data
taken from Petersen et al. (1998) – see Figure 5.9. This displays a gentler stall than
typical two-dimensional data, so there is no significant reduction in blade out-of-
plane bending moment as the blade goes into stall. Above about 20 m/s, the out-of-
plane bending moment begins to increase progressively once again as drag begins
to become significant. The predicted variation of blade 12 m radius out-of-plane
bending moment with wind speed is plotted out for a 0.2 shear exponent and a
range of yaw angles on Figure 7.9, with the yaw direction defined as positive when
the lateral component of air flow with respect to the rotor disc is in the same
direction as the blade movement at zero azimuth (i.e., at 12 o’clock). The effect of
this increase in relative velocity outweighs that of the reduction of angle of attack at
wind speeds beyond stall, so the bending moment at 08 azimuth is increased by
negative yaw. Maximum moments occur at negative yaw angles and 08 azimuth
rather than at positive yaw angles and 1808 azimuth, because wind shear augments
the wind speed in the former case. Also plotted is the variation of bending moment
with wind speed for a 138 shaft tilt with respect to flow and 908 azimuth, which is
the critical configuration for load cases not involving a change in wind direction.
Considering the deterministic load cases 1.3 and 1.5 to 1.9 initially, it is interesting
to note that the maximum out-of-plane bending moments lie within a relatively close
range in four of the six cases. It should be pointed out that, in the grid-loss case, the
bending moment depends on the rotor acceleration after loss of load, which is largely
determined by rotor inertia and the time delay to tip brake deployment. The bending
moment quoted is a notional one, based on a generous 1.5 s time delay until full
deployment and an inertia value calculated for a fibreglass rotor. With lighter rotors,

160

50 yaw,
140 Full-line curves are for 0 deg azimuth 0 azimuth 20 yaw,
12 m radius out-of-plane bending moment (kNm) 100 40 yaw, 0 yaw, 180 azimuth azimuth
Shear exponent = 0.2
Rotational speed = 30 r.p.m.
0 azimuth
120
13 tilt,
90
0 yaw,
0 azimuth
0 azimuth
80
60
40

20 40 yaw, 180 azimuth 20 yaw, 180 azimuth

0
0 5 10 15 20 25 30 35 40 45
Wind speed (m/s)
Figure 7.9 Variation of 12 m Radius Out-of-plane Bending Moment with Wind Speed at
Various Yaw Angles for an Example 40 m Diameter Stall-regulated Machine with TR Blades