Page 168 - Mechanical Behavior of Materials

Section 4.9 Bending and Torsion Tests 169

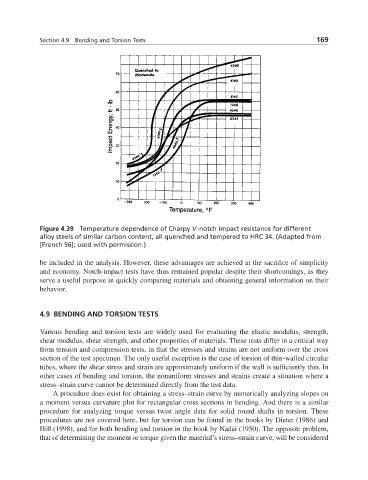
Figure 4.39 Temperature dependence of Charpy V-notch impact resistance for different
alloy steels of similar carbon content, all quenched and tempered to HRC 34. (Adapted from
[French 56]; used with permission.)

be included in the analysis. However, these advantages are achieved at the sacrifice of simplicity
and economy. Notch-impact tests have thus remained popular despite their shortcomings, as they
serve a useful purpose in quickly comparing materials and obtaining general information on their
behavior.

4.9 BENDING AND TORSION TESTS

Various bending and torsion tests are widely used for evaluating the elastic modulus, strength,
shear modulus, shear strength, and other properties of materials. These tests differ in a critical way
from tension and compression tests, in that the stresses and strains are not uniform over the cross
section of the test specimen. The only useful exception is the case of torsion of thin-walled circular
tubes, where the shear stress and strain are approximately uniform if the wall is sufficiently thin. In
other cases of bending and torsion, the nonuniform stresses and strains create a situation where a
stress–strain curve cannot be determined directly from the test data.
A procedure does exist for obtaining a stress–strain curve by numerically analyzing slopes on
a moment versus curvature plot for rectangular cross sections in bending. And there is a similar
procedure for analyzing torque versus twist angle data for solid round shafts in torsion. These
procedures are not covered here, but for torsion can be found in the books by Dieter (1986) and
Hill (1998), and for both bending and torsion in the book by Nadai (1950). The opposite problem,
that of determining the moment or torque given the material’s stress–strain curve, will be considered