Page 88 - Petroleum Production Engineering, A Computer-Assisted Approach

Guo, Boyun / Computer Assited Petroleum Production Engg 0750682701_chap06 Final Proof page 80 3.1.2007 8:40pm Compositor Name: SJoearun

6/80 PETROLEUM PRODUCTION ENGINEERING FUNDAMENTALS
Table 6.8 Solution Given by WellheadNodalOil-HB.xls
WellheadNodalOil-HB.xls
Description: This spreadsheet calculates operating point using Hagedorn–Brown correlation.
Instruction: (1) Select a unit system; (2) update parameter values in the Input data section; (3) click Solution
button; and (4) view result in the Solution section and charts.
Input data U.S. Field units SI units
Depth (D): 7,000 ft
Tubing inner diameter (d ti ): 3.5 in.
Oil gravity (API): 45 8API
Oil viscosity (m o ): 0.5 cp
Production gas–liquid ratio: 500 scf/bbl
Gas-specific gravity (g g ): 0.7 air ¼ 1
Choke size (S): 32 1/64 in.
Flowing tubing head temperature (t hf ): 80 8F
Flowing temperature at tubing shoe (t wf ): 150 8F
Water cut: 10%
Reservoir pressure (p e ): 4,000 psia
Bubble-point pressure (p b ): 3,800 psia
Productivity above bubble point (J*): 5 stb/d-psi
Choke flow constant (C): 10.00
Choke gas–liquid ratio exponent (m): 0.546
Choke-size exponent (n): 1.89
Solution q (stb/d) p wf (psia) p hf (psia)
WPR CPR
0 3,996 0
1,284 3,743 2,726 546
2,568 3,474 2,314 1,093
3,852 3,185 1,908 1,639
5,136 2,872 1,482 2,185
6,420 2,526 1,023 2,732
7,704 2,135 514 3,278
8,988 1,674 0 3,824

Equations (6.26) through (6.29) contain (4n 1) equa- p kf 1 , p kf 2 , .. . p kf n
tions. For a given flowing pressure p hf n at the top of
lateral n, the following (4n 1) unknowns can be solved p hf 1 , p hf 2 , .. . p hf n 1
from the (4n 1) equations: Then the production rate of the multilateral well can be
determined by
q 1 , q 2 , .. . q n
X
n
q ¼ q i : (6:30)
p wf 1 , p wf 2 , .. . p wf n
i¼1
4,500
WPR
4,000
CPR
3,500
Wellhead Pressure (psia) 2,500
3,000

2,000
1,500

1,000
500

0
0 1,000 2,000 3,000 4,000 5,000 6,000 7,000 8,000 9,000
Liquid Production Rate (bbl/d)

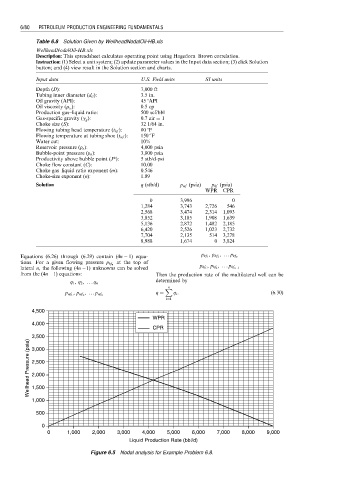
Figure 6.5 Nodal analysis for Example Problem 6.8.