Page 342 - Adsorption, Ion Exchange & Catalysis- 2007, Elsevier - Copy

Else_AIEC-INGLE_cH004.qxd 7/1/2006 6:54 PM Page 338
338 4. Adsorption and Ion Exchange

0.65
0.6

0.55

0.5
stoich
X
0.45
S
0.4
F
0.35
0 0.2 0.4 0.6 0.8 1
La

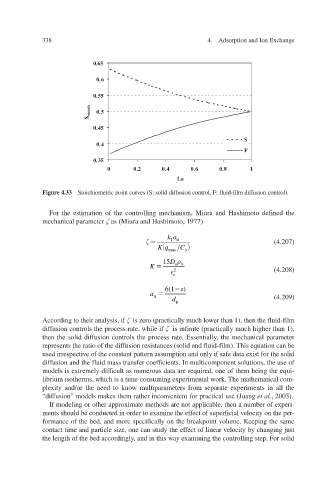
Figure 4.33 Stoichiometric point curves (S: solid diffusion control, F: fluid-film diffusion control).

For the estimation of the controlling mechanism, Miura and Hashimoto defined the
mechanical parameter as (Miura and Hashimoto, 1977)
ka
fu (4.207)
Kq C
max o
15 D
K sb
r 2 (4.208)
o
6(1 )
a u
d (4.209)
p
According to their analysis, if is zero (practically much lo then the fluid-f wer than 1), ilm
diffusion controls the process rate, while if is infinite (practically much higher than 1),
then the solid diffusion controls the process rate. Essentially the mechanical parameter
,
represents the ratio of the diffusion resistances (solid and fluid-film). This equation can be
used irrespective of the constant pattern assumption and only if safe data exist for the solid
diffusion and the fluid mass transfer coeficients. In multicomponent solutions, the use of f
f
models is extremely dificult as numerous data are required, one of them being the equi-
librium isotherms, which is a time-consuming e The mathematical com- xperimental w ork.
plexity and/or the need to know multiparameters from separate experiments in all the
“diffusion” models makes them rather inconenient for practical use (Juang v et al ., 2003).
If modeling or other approximate methods are not applicable, then a number of e xperi-
ments should be conducted in order to examine the effect of superficial velocity on the per-
formance of the bed, and more specifically on the breakpoint volume. Keeping the same
contact time and particle size, one can study the effect of linear velocity by changing just
ay e xamining the controlling step. For solid the length of the bed accordingly, and in this w