Page 279 - Applied Statistics And Probability For Engineers

c07.qxd 5/15/02 10:18 M Page 237 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

7-3 METHODS OF POINT ESTIMATION 237

–31.94
0.087
–31.96 –32.106
–31.98 0.085 –32.092
Log likelihood –32.02 0.083 –32.064
–32.078
–32.00
–32.04
–32.05
–32.06
–32.08 λ 0.081 –32.036 –31.997
–32.10 –32.022
0.087 0.079 –32.009
1.86
0.085 1.82
0.083 1.78 –31.995
λ 0.081 1.70 1.74 0.077
0.079 1.66 r
0.077
1.62 0.075
0.075 1.58
1.58 1.62 1.66 1.70 1.74 1.78 1.82 1.86
r
(a) (b)
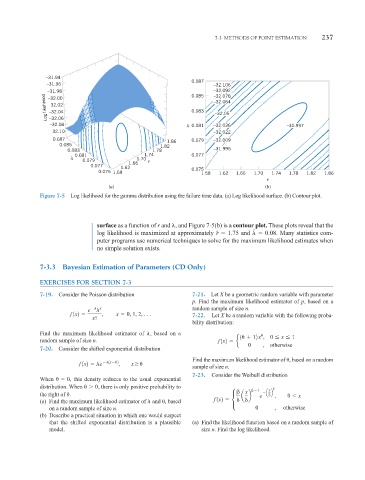
Figure 7-5 Log likelihood for the gamma distribution using the failure time data. (a) Log likelihood surface. (b) Contour plot.

surface as a function of r and , and Figure 7-5(b) is a contour plot. These plots reveal that the
ˆ
log likelihood is maximized at approximately r ˆ 1.75 and 0.08 . Many statistics com-
puter programs use numerical techniques to solve for the maximum likelihood estimates when
no simple solution exists.

7-3.3 Bayesian Estimation of Parameters (CD Only)

EXERCISES FOR SECTION 7-3

7-19. Consider the Poisson distribution 7-21. Let X be a geometric random variable with parameter
p. Find the maximum likelihood estimator of p, based on a

e x random sample of size n.
f 1x2 , x 0, 1, 2, . . . 7-22. Let X be a random variable with the following proba-
x!
bility distribution:

Find the maximum likelihood estimator of , based on a
1 12 x , 0 x 1
random sample of size n. f 1x2 e
0 , otherwise
7-20. Consider the shifted exponential distribution
Find the maximum likelihood estimator of , based on a random
f 1x2 e 1x 2 , x
sample of size n.
7-23. Consider the Weibull distribution

When 0, this density reduces to the usual exponential
distribution. When 0 , there is only positive probability to
x 1 x
the right of . a b e a b 0 x
,

(a) Find the maximum likelihood estimator of and , based f 1x2 •
on a random sample of size n. 0 , otherwise
(b) Describe a practical situation in which one would suspect
that the shifted exponential distribution is a plausible (a) Find the likelihood function based on a random sample of
model. size n. Find the log likelihood.