Page 289 - Calculus Demystified

276

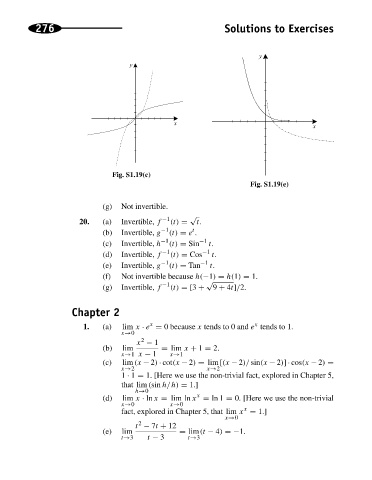
Fig. S1.19(c) Solutions to Exercises
Fig. S1.19(e)

(g) Not invertible.
√
20. (a) Invertible, f −1 (t) = t.
t
(b) Invertible, g −1 (t) = e .
(c) Invertible, h −1 (t) = Sin −1 t.
(d) Invertible, f −1 (t) = Cos −1 t.
(e) Invertible, g −1 (t) = Tan −1 t.
(f) Not invertible because h(−1) = h(1) = 1.
√
(g) Invertible, f −1 (t) =[3 + 9 + 4t]/2.

Chapter 2
x
x
1. (a) lim x · e = 0 because x tends to 0 and e tends to 1.
x→0
2
x − 1
(b) lim = lim x + 1 = 2.
x→1 x − 1 x→1
(c) lim (x − 2) · cot(x − 2) = lim [(x − 2)/ sin(x − 2)]· cos(x − 2) =
x→2 x→2
1 · 1 = 1. [Here we use the non-trivial fact, explored in Chapter 5,
that lim (sin h/h) = 1.]
h→0
x
(d) lim x · ln x = lim ln x = ln 1 = 0. [Here we use the non-trivial
x→0 x→0
x
fact, explored in Chapter 5, that lim x = 1.]
x→0
2
t − 7t + 12
(e) lim = lim(t − 4) =−1.
t→3 t − 3 t→3