Page 175 - Carbonate Sedimentology and Sequence Stratigraphy

166 WOLFGANG SCHLAGER

The name “diffusion equation” refers to its original use in A)
calculating the mixing of solutions at the molecular level. In
sedimentology and geomorphology, the equation provides h
good approximations for the cumulative effect of many sep-
arate events of sedimentation and erosion. For instance,
the transfer of siliciclastic sediment from a terrestrial source
across the coastal zone into an ocean basin is well described x
by the diffusion equation.
The diffusion equation is the centerpiece of the STRATA
program. The equation states that the time rate of change in B)
height at a given point is proportional to the second deriva- h
tive of the height with respect to the horizontal distance. It is x
written as a partial derivative because the second horizontal x
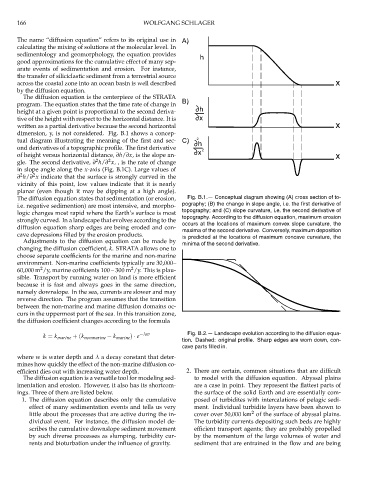
dimension, y, is not considered. Fig. B.1 shows a concep-
tual diagram illustrating the meaning of the first and sec- C) 2 h
ond derivatives of a topographic profile. The first derivative 2
of height versus horizontal distance, ∂h/∂x, is the slope an- x x
2
2
gle. The second derivative, ∂ h/∂ x,, is therate ofchange
in slope angle along the x-axis (Fig. B.1C). Large values of
2
2
∂ h/∂ x indicate that the surface is strongly curved in the
vicinity of this point, low values indicate that it is nearly
planar (even though it may be dipping at a high angle).
The diffusion equation states that sedimentation (or erosion, Fig. B.1.— Conceptual diagram showing (A) cross section of to-
i.e. negative sedimention) are most intensive, and morpho- pography; (B) the change in slope angle, i.e. the first derivative of
logic changes most rapid where the Earth’s surface is most topography; and (C) slope curvature, i.e. the second derivative of
strongly curved. In a landscape that evolves according to the topography. According to the diffusion equation, maximum erosion
occurs at the locations of maximum convex slope curvature, the
diffusion equation sharp edges are being eroded and con-
maxima of the second derivative. Conversely, maximum deposition
cave depressions filled by the erosion products. is predicted at the locations of maximum concave curvature, the
Adjustments to the diffusion equation can be made by
minima of the second derivative.
changing the diffusion coefficient, k. STRATA allows one to
choose separate coefficients for the marine and non-marine
environment. Non-marine coefficients typically are 30,000–
2
2
60,000 m /y, marine cofficients 100 – 300 m /y. This is plau-
sible. Transport by running water on land is more efficient
because it is fast and always goes in the same direction,
namely downslope. In the sea, currents are slower and may
reverse direction. The program assumes that the transition
between the non-marine and marine diffusion domains oc-
curs in the uppermost part of the sea. In this transition zone,
the diffusion coefficient changes according to the formula

k = k marine +(k nonmarine − k marine ) · e −λw Fig. B.2.— Landscape evolution according to the diffusion equa-
tion. Dashed: original profile. Sharp edges are worn down, con-
cave parts filled in.
where w is water depth and λ a decay constant that deter-
mines how quickly the effect of the non-marine diffusion co-
efficient dies out with increasing water depth. 2. There are certain, common situations that are difficult
The diffusion equation is a versatile tool for modeling sed- to model with the diffusion equation. Abyssal plains
imentation and erosion. However, it also has its shortcom- are a case in point. They represent the flattest parts of
ings. Three of them are listed below. the surface of the solid Earth and are essentially com-
1. The diffusion equation describes only the cumulative posed of turbidites with intercalations of pelagic sedi-
effect of many sedimentation events and tells us very ment. Individual turbidite layers have been shown to
2
little about the processes that are active during the in- cover over 50,000 km of the surface of abyssal plains.
dividual event. For instance, the diffusion model de- The turbidity currents depositing such beds are highly
scribes the cumulative downslope sediment movement efficient transport agents; they are probably propelled
by such diverse processes as slumping, turbidity cur- by the momentum of the large volumes of water and
rents and bioturbation under the influence of gravity. sediment that are entrained in the flow and are being