Page 187 - Chemical Process Equipment - Selection and Design
P. 187
7.6. THEORY AND CALCULATIONS OF GAS COMPRESSiON 159
In terms of a known isentropic efficiency the final temperature T,
then is found by trial from
T2
(AH)Jqs = 1 C; dT + AH; - AH;. (7.49)
Ti
In these equations the heat capacity C; is that of the ideal gas
state or that of the real gas near zero or atmospheric pressure. The
residual properties AS; and AH; are evaluated at (Pl, Tl) and AS;
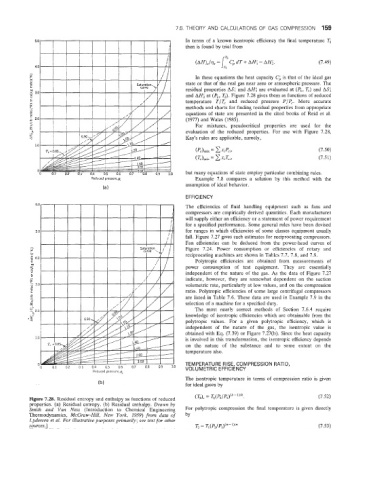
and AH; at (P2, TJ. Figure 7.28 gives them as functions of reduced
temperature T/T, and reduced pressure P/P,. More accurate
methods and charts for finding residual properties from appropriate
equations of state are presented in the cited books of Reid et al.
(1977) and Walas (1985).
For mixtures, pseudocritical properties are used for the
evaluation of the reduced properties. For use with Figure 7.28,
Kay’s rules are applicable, namely,
(7.50)
(7.51)
but many equations of state employ particular combining rules.
Example 7.8 compares a solution by this method with the
assumption of ideal behavior.
EFFICIENCY
The efficiencies of fluid handling equipment such as fans and
compressors are empirically derived quantities. Each manufacturer
will supply either an efficiency or a statement of power requirement
for a specified performance. Some general rules have been devised
for ranges in which efficiencies of some classes equipment usually
fall. Figure 7.27 gives such estimates for reciprocating compressors.
Fan efficiencies can be deduced from the power-head curves of
Figure 7.24. Power consumption or efficiencies of rotary and
reciprocating machines are shown in Tables 7.7, 7.8, and 7.9.
Polytropic efficiencies are obtained from measurements of
power consumption of test equipment. They are essentially
independent of the nature of the gas. As the data 0f Figure 7.27
indicate, however, they are somewhat dependent on the suction
volumetric rate, particularly at low values, and on the compression
ratio. Polytropic efficiencies of some large centrifugal compressors
are listed in Table 7.6. These data are used in Example 7.9 in the
selection of a machine for a specified duty.
The most nearly correct methods of Section 7.6.4 require
knowledge of isentropic efficiencies which are obtainable from the
polytropic values. For a given polytropic efficiency, which is
independent of the nature of the gas, the isentropic value is
obtained with Eq. (7.39) or Figure 7.27(b). Since the heat capacity
is involved in this transformation, the isentropic efficiency depends
on the nature of the substance and to some extent on the
temperature also.
TEMPERATURE RISE, COMPRESSION RATIO,
VOLUMETRIC EFFICIENCY
Reduced pressure.pr
The isentropic temperature in terms of compression ratio is given
tb) for ideal gases by
Figure 7.28. Residual entropy and enthalpy as functions of reduced (T& = TpyP1)‘k-””. (7.52)
properties. (a) Residual entropy. (b) Residual enthalpy. Drawn by
Smith and Van Ness (Introduction to Chemical Engineering For polytropic compression the final temperature is given directly
Thermodynamics, McGraw-Hill, New York, 1959) from data of bY
Lydersen et al. For illustrative purposes primarily; see text for other
sources.] T, = T&/Pl)‘”-l”” (7.53)