Page 18 - Complementarity and Variational Inequalities in Electronics

8 Complementarity and Variational Inequalities in Electronics

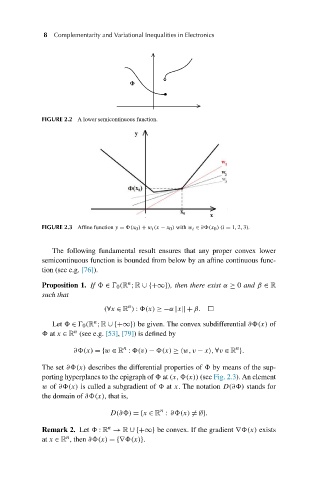
FIGURE 2.2 A lower semicontinuous function.

FIGURE 2.3 Affine function y = (x 0 ) + w i (x − x 0 ) with w i ∈ ∂ (x 0 ) (i = 1,2,3).

The following fundamental result ensures that any proper convex lower
semicontinuous function is bounded from below by an affine continuous func-
tion (see e.g. [76]).
n
Proposition 1. If ∈ 0 (R ;R ∪{+∞}), then there exist α ≥ 0 and β ∈ R
such that
n
(∀x ∈ R ) : (x) ≥−α x + β.
n
Let ∈ 0 (R ;R ∪{+∞}) be given. The convex subdifferential ∂ (x) of
n
at x ∈ R (see e.g. [53], [79]) is defined by
n
n
∂ (x) ={w ∈ R : (v) − (x) ≥
w,v − x ,∀v ∈ R }.
The set ∂ (x) describes the differential properties of by means of the sup-
porting hyperplanes to the epigraph of at (x, (x)) (see Fig. 2.3). An element
w of ∂ (x) is called a subgradient of at x. The notation D(∂ ) stands for
the domain of ∂ (x), that is,

n
D(∂ ) ={x ∈ R : ∂ (x) = ∅}.
n
Remark 2. Let : R → R ∪{+∞} be convex. If the gradient ∇ (x) exists
n
at x ∈ R , then ∂ (x) ={∇ (x)}.