Page 340 - Computational Statistics Handbook with MATLAB

Chapter 9: Statistical Pattern Recognition 329

0.25

0.2

0.15

0.1

0.05

0
−6 −4 −2 0 2 4 6 8
Feature − x
FI F IG URE G 9. RE 9. 6 6
U
6
GU
F F II GU RE RE 9. 9. 6
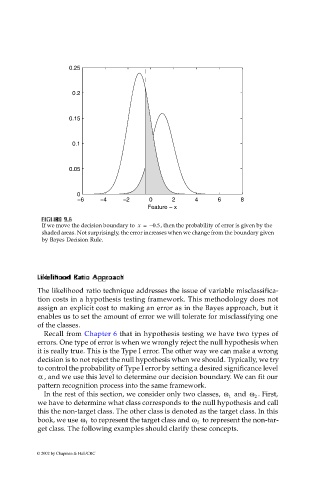
If we move the decision boundary to x = – 0.5 , then the probability of error is given by the
shaded areas. Not surprisingly, the error increases when we change from the boundary given
by Bayes Decision Rule.

Approach
Likelihood ikelihood ApproachApproach
LRatioikelihoodRatioApproach
LLikelihoodRatioRatio
The likelihood ratio technique addresses the issue of variable misclassifica-
tion costs in a hypothesis testing framework. This methodology does not
assign an explicit cost to making an error as in the Bayes approach, but it
enables us to set the amount of error we will tolerate for misclassifying one
of the classes.
Recall from Chapter 6 that in hypothesis testing we have two types of
errors. One type of error is when we wrongly reject the null hypothesis when
it is really true. This is the Type I error. The other way we can make a wrong
decision is to not reject the null hypothesis when we should. Typically, we try
to control the probability of Type I error by setting a desired significance level
α , and we use this level to determine our decision boundary. We can fit our
pattern recognition process into the same framework.
. First,
In the rest of this section, we consider only two classes, ω 1 and ω 2
we have to determine what class corresponds to the null hypothesis and call
this the non-target class. The other class is denoted as the target class. In this
to represent the non-tar-
book, we use ω 1 to represent the target class and ω 2
get class. The following examples should clarify these concepts.

© 2002 by Chapman & Hall/CRC