Page 138 -

3.4 Fourier transforms 117

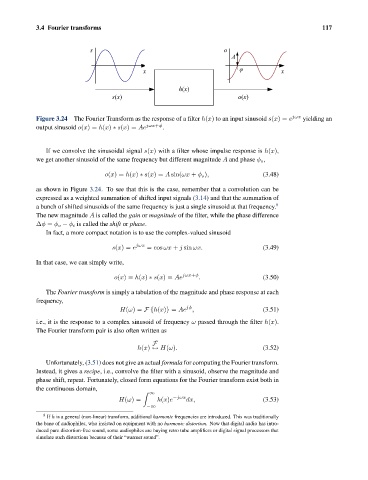
s o
A

x ij x

h(x)
s(x) o(x)

Figure 3.24 The Fourier Transform as the response of a filter h(x) to an input sinusoid s(x)= e jωx yielding an
output sinusoid o(x)= h(x) ∗ s(x)= Ae jωx+φ .

If we convolve the sinusoidal signal s(x) with a filter whose impulse response is h(x),
we get another sinusoid of the same frequency but different magnitude A and phase φ o ,

o(x)= h(x) ∗ s(x)= A sin(ωx + φ o ), (3.48)

as shown in Figure 3.24. To see that this is the case, remember that a convolution can be
expressed as a weighted summation of shifted input signals (3.14) and that the summation of
a bunch of shifted sinusoids of the same frequency is just a single sinusoid at that frequency. 8
The new magnitude A is called the gain or magnitude of the filter, while the phase difference
Δφ = φ o − φ i is called the shift or phase.
In fact, a more compact notation is to use the complex-valued sinusoid

s(x)= e jωx = cos ωx + j sin ωx. (3.49)

In that case, we can simply write,
o(x)= h(x) ∗ s(x)= Ae jωx+φ . (3.50)

The Fourier transform is simply a tabulation of the magnitude and phase response at each
frequency,
jφ
H(ω)= F{h(x)} = Ae , (3.51)
i.e., it is the response to a complex sinusoid of frequency ω passed through the filter h(x).
The Fourier transform pair is also often written as
F
h(x) ↔ H(ω). (3.52)

Unfortunately, (3.51) does not give an actual formula for computing the Fourier transform.
Instead, it gives a recipe, i.e., convolve the filter with a sinusoid, observe the magnitude and
phase shift, repeat. Fortunately, closed form equations for the Fourier transform exist both in
the continuous domain,
∞

H(ω)= h(x)e −jωx dx, (3.53)
−
8 If h is a general (non-linear) transform, additional harmonic frequencies are introduced. This was traditionally
the bane of audiophiles, who insisted on equipment with no harmonic distortion. Now that digital audio has intro-
duced pure distortion-free sound, some audiophiles are buying retro tube amplifiers or digital signal processors that
simulate such distortions because of their “warmer sound”.