Page 475 - Design for Six Sigma a Roadmap for Product Development

434 Chapter Twelve

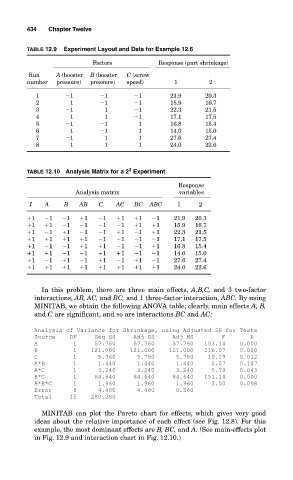
TABLE 12.9 Experiment Layout and Data for Example 12.6

Factors Response (part shrinkage)
Run A (booster B (booster C (screw
number pressure) pressure) speed) 1 2
1 1 1 1 21.9 20.3
2 1 1 1 15.9 16.7
3 1 1 1 22.3 21.5
4 1 1 1 17.1 17.5
5 1 1 1 16.8 15.4
6 1 1 1 14.0 15.0
7 1 1 1 27.6 27.4
8 1 1 1 24.0 22.6

3
TABLE 12.10 Analysis Matrix for a 2 Experiment
Response
Analysis matrix variables
I A B AB C AC BC ABC 1 2
1 1 1 1 1 1 1 1 21.9 20.3
1 1 1 1 1 1 1 1 15.9 16.7
1 1 1 1 1 1 1 1 22.3 21.5
1 1 1 1 1 1 1 1 17.1 17.5
1 1 1 1 1 1 1 1 16.8 15.4
1 1 1 1 1 1 1 1 14.0 15.0
1 1 1 1 1 1 1 1 27.6 27.4
1 1 1 1 1 1 1 1 24.0 22.6

In this problem, there are three main effects, A,B,C, and 3 two-factor
interactions, AB, AC, and BC, and 1 three-factor interaction, ABC. By using
MINITAB, we obtain the following ANOVA table; clearly, main effects A, B,
and C are significant, and so are interactions BC and AC:

Analysis of Variance for Shrinkage, using Adjusted SS for Tests
Source DF Seq SS Adj SS Adj MS F P
A 1 57.760 57.760 57.760 103.14 0.000
B 1 121.000 121.000 121.000 216.07 0.000
C 1 5.760 5.760 5.760 10.29 0.012
A*B 1 1.440 1.440 1.440 2.57 0.147
A*C 1 3.240 3.240 3.240 5.79 0.043
B*C 1 84.640 84.640 84.640 151.14 0.000
A*B*C 1 1.960 1.960 1.960 3.50 0.098
Error 8 4.480 4.480 0.560
Total 15 280.280

MINITAB can plot the Pareto chart for effects, which gives very good
ideas about the relative importance of each effect (see Fig. 12.8). For this
example, the most dominant effects are B, BC, and A. (See main-effects plot
in Fig. 12.9 and interaction chart in Fig. 12.10.)