Page 296 - Digital Analysis of Remotely Sensed Imagery

258 Cha pte r Se v e n

7.2.1 Euclidean Spectral Distance
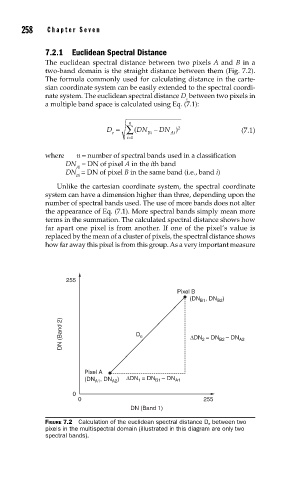
The euclidean spectral distance between two pixels A and B in a
two-band domain is the straight distance between them (Fig. 7.2).
The formula commonly used for calculating distance in the carte-
sian coordinate system can be easily extended to the spectral coordi-
nate system. The euclidean spectral distance D between two pixels in
e
a multiple band space is calculated using Eq. (7.1):

n
D = ∑ ( DN − DN ) 2 (7.1)
e Bi Ai
i=1
where n = number of spectral bands used in a classification
DN = DN of pixel A in the ith band
Ai
DN = DN of pixel B in the same band (i.e., band i)
Bi
Unlike the cartesian coordinate system, the spectral coordinate
system can have a dimension higher than three, depending upon the
number of spectral bands used. The use of more bands does not alter
the appearance of Eq. (7.1). More spectral bands simply mean more
terms in the summation. The calculated spectral distance shows how
far apart one pixel is from another. If one of the pixel’s value is
replaced by the mean of a cluster of pixels, the spectral distance shows
how far away this pixel is from this group. As a very important measure

255
Pixel B
(DN , DN )
B1
B2
DN (Band 2) D e ΔDN = DN B2 – DN A2

2

Pixel A
(DN , DN ) ΔDN = DN B1 – DN A1
1
A2
A1
0
0 255
DN (Band 1)
FIGURE 7.2 Calculation of the euclidean spectral distance D e between two
pixels in the multispectral domain (illustrated in this diagram are only two
spectral bands).