Page 314 - Dynamics of Mechanical Systems

0593_C09_fm Page 295 Monday, May 6, 2002 2:50 PM

Principles of Impulse and Momentum 295

Similarly, from Eq. (9.6.8), if the angular impulse J on a particle is zero, we have:
Q

∆A = 0 or A t () = A t () (9.7.2)
Q Q 2 Q 1
Therefore, if the angular impulse is zero, the angular momentum is the same at the
beginning and end of the impulse time interval and thus throughout the time interval;
hence, the angular momentum is constant, or conserved. Similar statements can be made
for sets of particles and for a rigid body using Eqs. (9.6.16), (9.6.36), and (9.6.37).
Observe that because linear and angular impulses are vectors, they may be nonzero but
still have zero projection in some directions. In such cases, the projection of the momenta
along those directions is conserved. For example, if n is a unit vector such that:

In⋅= 0 (9.7.3)

then, from Eq. (9.5.3), we have:
( ) L()⋅= L()⋅ n (9.7.4)
∆Ln⋅= 0 or
t
n
t
2
1
That is, the linear momentum is conserved in the n direction. Similar results occur for
angular momenta.

9.8 Examples

Example 9.8.1: A Sliding Collar
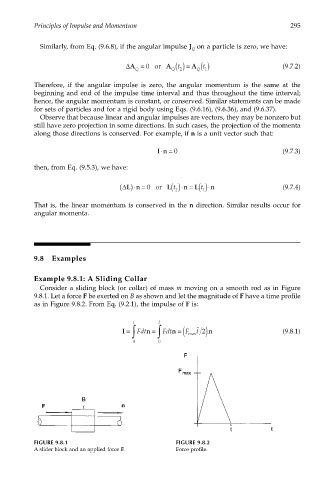
Consider a sliding block (or collar) of mass m moving on a smooth rod as in Figure
9.8.1. Let a force F be exerted on B as shown and let the magnitude of F have a time profile
as in Figure 9.8.2. From Eq. (9.2.1), the impulse of F is:

t t ˆ
I = ∫ Fdt n = ∫ Fdt n = ( F max t ˆ n ) 2 (9.8.1)
0 0

FIGURE 9.8.1 FIGURE 9.8.2
A slider block and an applied force F. Force profile.